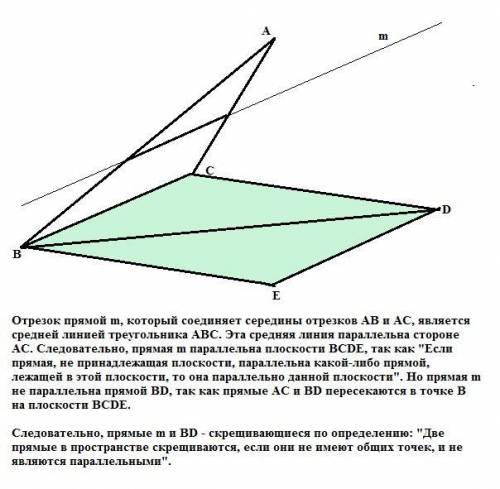
Прямые BD и m - скрещивающиеся прямые.
Объяснение:
Отрезок прямой m, который соединяет середины отрезков AB и AC, является средней линией треугольника АВС. Эта средняя линия параллельна стороне АС. Следовательно, прямая m параллельна плоскости ВСDE, так как "Если прямая, не принадлежащая плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то она параллельно данной плоскости". Но прямая m не параллельна прямой BD, так как прямые АС и BD пересекаются в точке В на плоскости BCDE.
Следовательно, прямые m и BD - скрещивающиеся по определению: "Две прямые в пространстве скрещиваются, если они не имеют общих точек, и не являются параллельными".
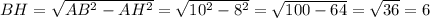

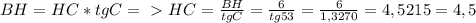
Объяснение:
ЗАДАЧА 70
обозначим вершины трапеции А В С Д с высотой СН, с основаниями ВС и АД и средней линией КЕ.
СН делит основании АД:
обозначим эти пропорции как 3х и 2х. СН делит АД так, что АН=ВС=3х. Составим уравнение используя формулу нахождения средней линии трапеции:
4х=12
х=12÷4=3
тогда ВС=3×3=9см, АД=3х+2х=5х=5×3=15см
ОТВЕТ: ВС=9см, АД=15см
ЗАДАЧА 71
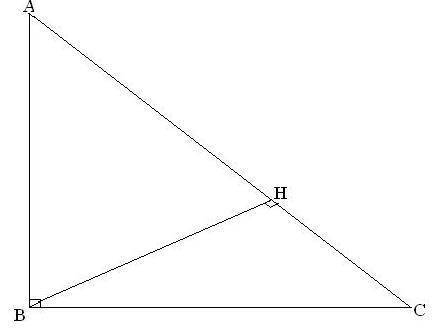
Обозначим вершины трапеции А В С Д с основаниями ВС и АД и диагональю АС. Рассмотрим ∆АВС. Если АВ=ВС, то ∆АВС - равнобедренный, поэтому <ВАС=<ВСА, а также <ВСА=<САД как внутренние разносторонние, поэтому диагональ АС является биссектрисой угла А, значит угол А=23×2=46°. Сумма углов трапеции прилегающих к одной боковой стороне составляют 180°, поэтому <В=<С=180–46=134°. Так как трапеция равнобедренная то <А=<Д=46°, <В=<С=134°
ОТВЕТ: 46°, 134°