Zmeura1204
Объяснение:
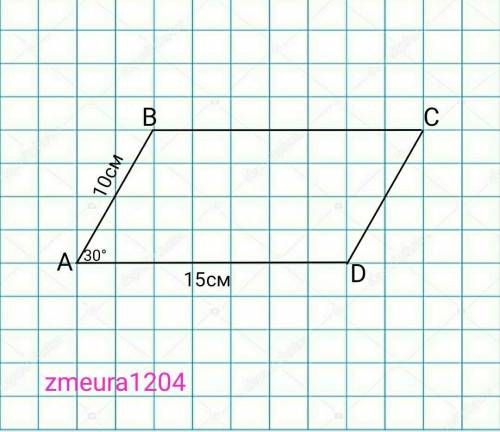
1)
Дано:
АВСD-параллелограм
AB=10см
AD=15см
<А=30°
S=?
_______
Решение
S=AB*AD*sin<A
sin<30°=1/2
S=1/2*10*15=75см²
ответ: 75см²
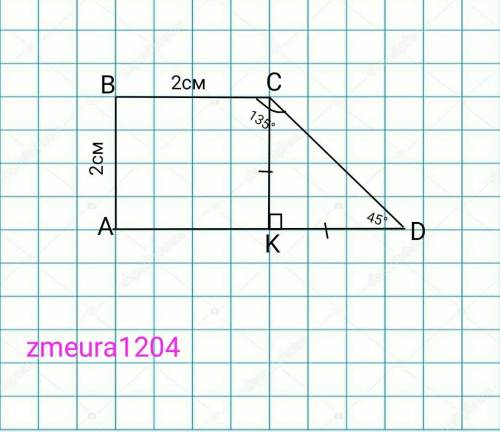
2)
Дано:
ABCD- трапеция
<ВАD=<ABC=90°
<BCD=135°
BC=2см
АВ=2см
S(ABCD)=?
______
Решение
Сумма углов прилежащих к боковой стороне трапеции равна 180°
<CDK=180°-<BCD=180°-135°=45°
Проведём высоту СК.
∆CKD- прямоугольный равнобедренный треугольник (углы при основании равны. <СКD=90°; <CDK=45°; <KCD=90°-45°=45°)
CK=KD=AB=2см
АD=BC+KD=2+2=4см.
S(ABCD)=CK(BC+AD)/2=2(2+4)/2=6см²
ответ: 6см²
Конус;
Осевое сечение конуса - равнобедренный △АВС;
∠В = 120°;
АВ = ВС = 6 см.
Найти:V - ? (см³).
Решение:Проведём высоту ВН. Получилось два равных прямоугольных треугольника АВН и СВН (их равенство можно также доказать по всем признакам равенства прямоугольных треугольников, исходя из того, что △АВС - равнобедренный).
"Высота, проведённая из вершины равнобедренного треугольника к основанию равнобедренного треугольника, является медианой и биссектрисой".
⇒∠АВН = ∠СВН = 120°/2 = 60°, так как ВН - биссектриса.
СН/СВ = sin ∠CBH ⇒ R = CH = CB ⋅ sin 60˚ = 6 ⋅ √3/2 = 3√3 (см).
Найдём высоту ВН, по теореме Пифагора:
с = √(a² + b²) ⇒ a = √(c² - b²), где a и b - катеты, c - гипотенуза.
a = √(6² - (3√3)²) = √9 = 3 (см).
Итак, ВН = 3 (см).
V = 1/3πR²h = π(1/3 ⋅ (3√3)² ⋅ 3) = 27π (см³).
ответ: 27π (см³).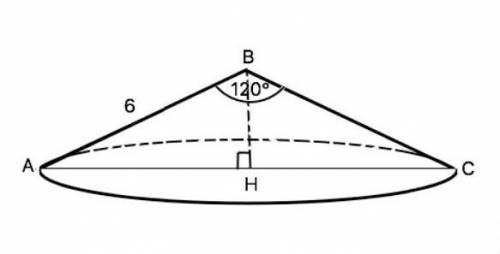
Привет!
OB-x
OD-2+x
угол BCA=CAD
угол ODA=угол OBC
Из этого следует,что треугольник BCO подобен треугольнику DAO
Составляем соотношение
OB/DO=BC/DA
дальше уравнение
x/2+x=6/9
12+6x=9x
x=4-OB
OD=6