ОА*ОВ +ОА*ОД+ ОС*ОД+ОС*ОВ) =0,5 sin X* АС*ВД
При пересечении двух прямых образуются только углы двух видов: смежные и вертикальные.
Перпендикулярные прямые рассматривать смысла нет: все углы по 90° и условие не выполняется, поэтому есть 2 тупых и 2 острых угла.
У смежных углов сумма равна 180°.
То есть даже на примере:
∠1 смежен с ∠3 и ∠4, то есть ∠1+∠3=180°, ∠1+∠4=180°
Аналогично ∠2 смежен с теми же углами. И ∠1=∠2.
И это явно не могут быть 2 тупых угла, так как они как вертикальные равны между собой, но если ∠3+∠4=140° и ∠3=∠4, то ∠3=∠4=70°, а они тупые, то есть такого быть не может. Поэтому это могут быть только ∠1 и ∠2, которые равны по 70° и являются друг для друга вертикальными.
Что и требовалось доказать.
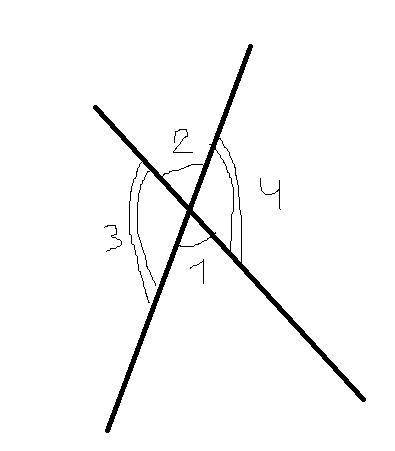
При пересечении двух прямых образуются только углы двух видов: смежные и вертикальные.
Перпендикулярные прямые рассматривать смысла нет: все углы по 90° и условие не выполняется, поэтому есть 2 тупых и 2 острых угла.
У смежных углов сумма равна 180°.
То есть даже на примере:
∠1 смежен с ∠3 и ∠4, то есть ∠1+∠3=180°, ∠1+∠4=180°
Аналогично ∠2 смежен с теми же углами. И ∠1=∠2.
И это явно не могут быть 2 тупых угла, так как они как вертикальные равны между собой, но если ∠3+∠4=140° и ∠3=∠4, то ∠3=∠4=70°, а они тупые, то есть такого быть не может. Поэтому это могут быть только ∠1 и ∠2, которые равны по 70° и являются друг для друга вертикальными.
Что и требовалось доказать.

Пусть АВСД параллелограмм и его диагонали пересекаются в точек О. Тогда площадь параллелограмма равна сумме площадей тр-ков АОВ, ВОС, СОД и АОД. Пусть Угол АОД = Х, тогда угол ВОС =Х, Угол АОВ =180 -Х. угол СОД = 180-Х
Известно, что sin X = sin ( 180 -X)
площадь каждого тр-ка равна половине произведения двух его сторон на синус угла между ними, поэтому площадь параллелограмма равна
0,5 ОА*ОВ*sin X +0,5 ОА*ОД*sin X+ 0,5 ОС*ОД*sin X+
0,5 ОС*ОВ*= 0,5 sin X * ( ОА*ОВ +ОА*ОД+ ОС*ОД+ОС*ОВ) =
=0,5 sin X* АС*ВД ( группируя первой слагаемое со вторым. а третье с четвёртым и т. д)