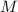, как выглядит на рисунку , так как 
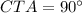, то около треугольника можно описать окружность такая что 
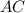будет диаметром , 
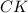биссектриса ,то 
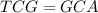, прямоугольник 
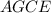в нем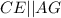 
, следовательно 
; 
; 
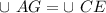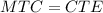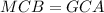откуда следует что равны по соответствующим дугам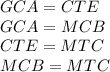 
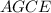является прямоугольник, авторы задачи видимо на этом и конструировали эту самую задачу.
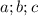и проделать операций которые описаны ниже,но оно будет объемным)
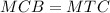, то есть что это действительно так , тогда должно выполнятся условие 
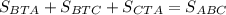, если это не так то предположение будет не верным , значит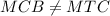 
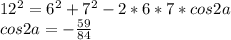
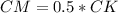, можно найти по формуле биссектрисы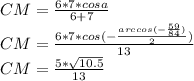 
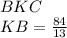
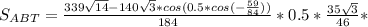
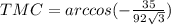(это когда находя угол 
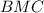, затем отнимая от 
) 
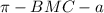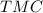, по теореме синусов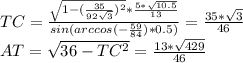 
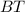по теореме косинусов так же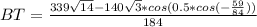 
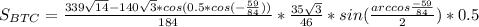
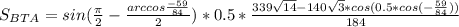
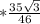
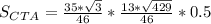
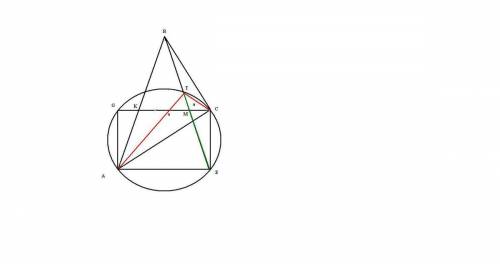
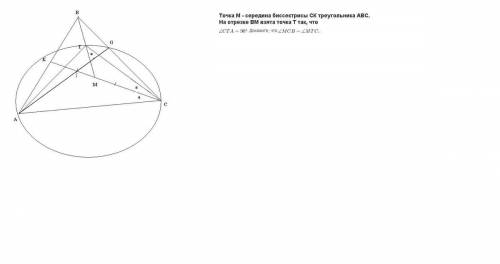
По условию, b = 8, α = 37°, γ=60°.
Тогда β = 180° - (α + γ) , тогда sin β = sin(180° - (α + γ)) = sin (α + γ)
По теореме синусов: b / sin β = c /sin γ, отсюда c = b · (sin γ / sin β)
Тогда площадь треугольника: S = 1/2 · b · c · sin α = b/2 · b · (sin γ / sin β) · sin α.
Таким образом S = (b2 · sin α · sin γ) / (2 · sin β)
S = [b2 · sin α · sin γ] / [2 · sin (α + γ)]
S = [64 · sin 37° · sin 60°] / [2 · sin 97°]
По таблице Брадиса:
sin 37° ≈ 0,602
sin 60° ≈ 0,866
sin 97° ≈ 0,993
S ≈ [64 · 0,602 · 0,866] / [2 · 0,993] ≈ 16,8
ответ ≈ 16,8
В
Объяснение:
Биссектриса треугольника и делит противоположную сторону на отрезки пропорциональные прилежащим сторонам треугольника, то есть АВ:АД=ВС:ДС. Обозначим АД=х, тогда ДС=18-х. Получаем
12:х=15:(18-х)
15*х=12*(18-х)
15*х+12*х=216
27*х=216
х=216:27
х=8
АД=8 см.