Дано:
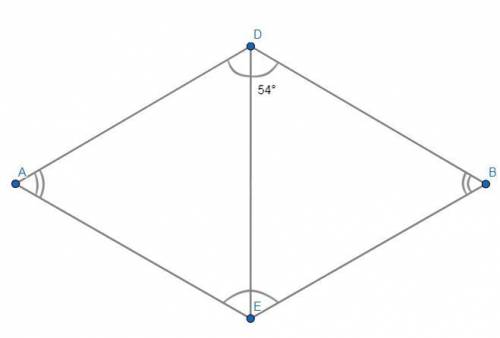
ADBE - ромб.
DE - диагональ.
∠EDB = 54°.
Найти:
∠ADB = ?
∠DBE = ?
∠BEA = ?
∠EAD = ?
1) Диагонали ромба являются биссектрисами углов, из которых они исходят. Поэтому, ∠ADB = 2*∠EDB = 2*54° = 108°.
2) Сумма двух углов параллелограмма (ромб - частный случай параллелограмма), прилежащих к одной стороне, равна 180°. Следовательно, ∠ADB+∠DBE = 180° ⇒ ∠DBE = 180°-∠ADB ⇒ ∠DBE = 180°-108° ⇒∠DBE = 72°.
3) Противоположные углы параллелограмма равны (на рисунке выделены дугами). Следовательно, ∠ADB = ∠BEA = 108°, ∠DBE = ∠EAD = 72°.
ответ: 108°, 72°, 108°, 72°.
(х+2)²+(у-1)²=9 - это окружность с центром в т. O(-2, 1) и радиусом r=3.
Координаты середины отрезка ОА: x=(x1+x2)/2=(-2+4)/2=1, y=(y1+y2)/2=(1+1)/2=1. Подставив эти значения в уравнение окружности, убедимся, что они удовлетворяют этому уравнению:
(1+2)²+(1-1)²=9.
Следовательно, окружность проходит через середину OA, ч.т.д..