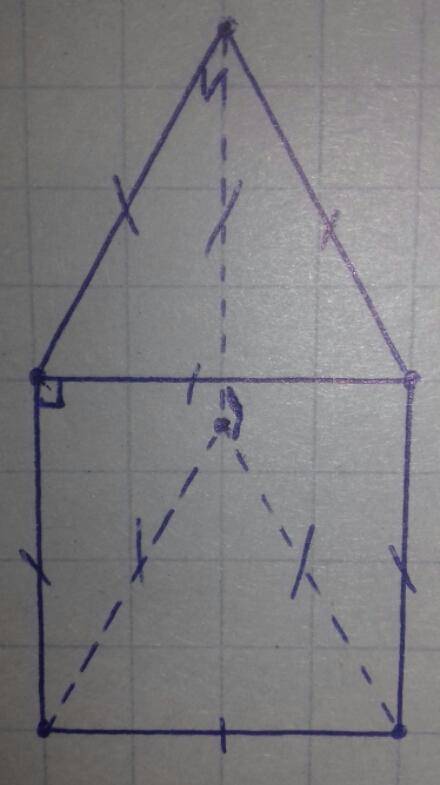
Высотой пирамиды РАВС есть боковое ребро РА, принадлежащее двум вертикальным граням АРС и АРВ.
Поведём сечение пирамиды вертикальной плоскостью, проходящей через высоту пирамиды перпендикулярно стороне ВС в точке Д.
Отрезок АД как высота правильного треугольника равен:
АД = a*cos30° = a√3/2.
Тогда высота РД третьей боковой грани равна:
РД = АД/cosα = a√3/(2cosβ).
Теперь находим высоту пирамиды РА:
Н = РА = АД*tgβ = (a√3/2)*tgβ.
Площадь двух вертикальных граней равна:
Sв = 2*(1/2)*а*Н = (a²√3/2)*tgβ.
Площадь наклонной грани равна:
Sн = (1/2)*а*РД = (1/2)a*(a√3/(2cosβ)) = a²√3/(4cosβ).
Площадь боковой поверхности равна:
Sбок = Sв + Sн = ((a²√3/2)*tgβ) + (a²√3/(4cosβ)) = a²√3((tgβ/2) + (1/4cosβ))
В такой призме боковые грани это равные квадраты (все стороны равны, а угол между смежными сторонами равен 90° т.к. призма прямая). Всего 3 боковых грани (призма треугольная). Площадь одной боковой грани будет 75м²÷3=25м², а т.к. это площадь квадрата, то его сторона равна 5м (5м·5м=25м²). Все рёбра призмы равны, поэтому в основаниях будут равные, равносторонние треугольники, со стороной равной 5м. Площадь одного такого треугольника можно найти по формуле площади для равностороннего треугольника, через сторону.
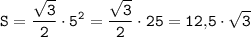 м².
м².
ответ: 12,5·√3 м².