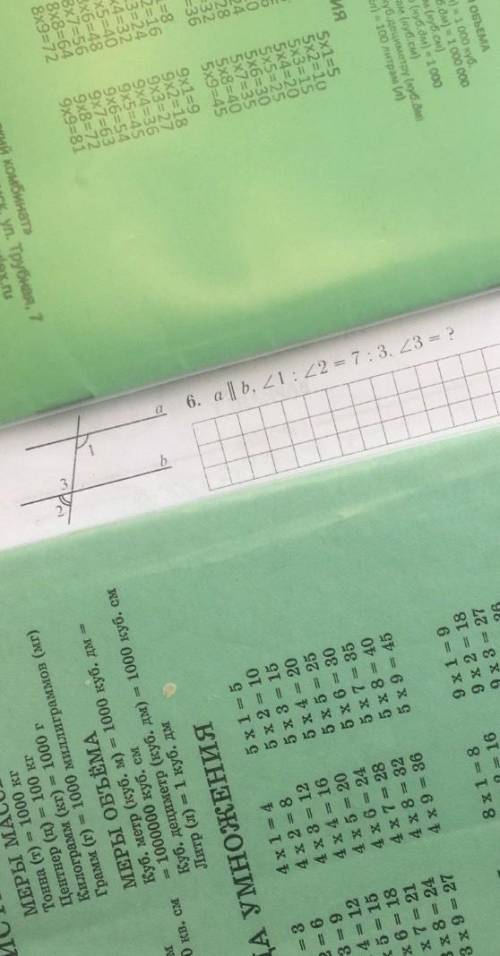
Объяснение:
Пусть <1=7х
<2=3х
<4=<2=3х - как вертикальные
Сумма внутренних односторонних углов равна 180 градусов :
<1+<4=180
7х+3х=180
10х=180
Х=180:10
Х=18
<1=7×18=126 градусов
<2=3×18=54 градуса
<3=<1=126 градусов как внутренние накрест лежащие

1.Площадь основания делим на 2 равных треугольника и прямоугольника. Один катет треугольника: (10-4):2=3.По теореме Пифагора второй катет равен 4-ём (3;4;5 -Пифагоровы числа) Площадь трапеции равно 1/2*(4+10)*4=28.У нас 2 основания: 28*2=56.
Боковая площадь равно сумме 4-х боковых прямоугольников, т. е. перемитру основания умножено на высоту примы (в данном случае на боковую ребру призмы, т. к. призма-прямая) . (10+5+5+4)*10=24*10=240.
Полная поверхность: 56+240=296.
ответ: 296 см^2
К
Объяснение:
Нет
Объяснение:
Общее уравнение прямой в пространстве ax + by + cz + d = 0, где a,b,c, d -- числа.
Через любые две точки можно построить прямую и притом только одну. Допустим, что через точки A и B проходит прямая. Найдем ее уравнение: для этого подставим координаты в общее уравнение и найдем коэффициенты.
Подставляем в уравнение координаты точки A(1,0,0):
a*1 + b*0 + c*0 + d = 0
a + d = 0
Подставляем в уравнение координаты точки и(1,2,2):
Подставляем в уравнение координаты точки A(1,0,0):
a*1 + b*2 + c*2 + d = 0
a + 2b + 2c + d = 0
Объединим 2 полученных уравнения в систему и решим ее:
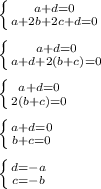
Пусть a = 1, b = 1, тогда d = -1, c = -1. Получаем уравнение прямой, проходящей через точки A и B:
1*x + 1*y -1*z - 1 = 0
x + y - z - 1 = 0.
Если точка C, лежит на одной прямой с точками A и B, то ее координаты должны удовлетворять полученному уравнению прямой. Проверим:
2 + 2 - 2 - 1 ≠ 0 ⇒ C не лежит на одной прямой с точками A и B
<3=126°
Объяснение:
<1=<3, внутренние накрест лежащие.
Значит
<3:<2=7:3
Пусть градусная мера угла <3 будет 7х°; тогда градусная мера угла <2 будет 3х°.
<3+<2=180°, смежные углы
Составляем уравнение
7х+3х=180°
10х=180
х=180/10
х=18
7*18=126° градусная мера угла <3