один кут 65, второй 115
Объяснение:
1)x+x+50=180
2x=130
x=65
2)65+50=115
Есть пирамида АВСДА1В1С1Д1, где АВСД - нижнее основание, О - центр нижнего основания, т.Л - середина стороны СД. Аналогично назовем Л1 и О1 для верхнего основания А1В1С1Д1. Восстановим вершину усеченной пирамиды и назовем ее т.К.
Рассмотрим прямоугольный треугольник КЛО: т.к. КО - катет, лежащий против угла КЛО=30 градусов, то КЛ=2*КО. ОЛ=АД/2=24/2=12. Примем КО за х. Тогда КО^2+ОЛ^2=КЛ^2; х^2+12^2=(2х)^2; х=КО=4*корень из 3; КЛ=8*корень из 3.
Из подобия треугольников КЛО и КЛ1О1:
ОЛ/О1Л1=КО/КО1, отсюда КО1=О1Л1*КО/ОЛ=(20/2)*(4*корень из 3)/12=10/корень из 3
V усеч. = V(КАВСД) - V(КА1В1С1Д1)=S(АВСД)*КО/3- S(А1В1С1Д1)*КО1/3=
=24*24*4*(корень из 3)/3-20*20*(10/корень из 3)/3=2912/(3*корень из 3)
Найти: d
По основному тригонометрическому свойству:
cos²(BAO)+sin²(BAO)=1
(0,6)²+sin²(BAO)=1
sin²(BAO)=0,64
Совокупность:
sin(BAO)=0,8
sin(BAO)=–0,8
Так как угол ВАО меньше 180°, то sin(BAO)=0,8
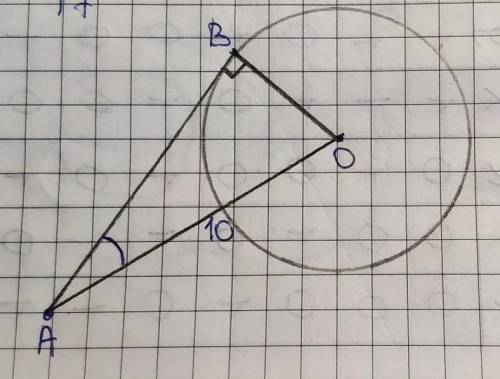
Проведем ОВ.
ОВ перпендикулярен АВ, так как радиус окружности, проведенный к точке касания касательной, перпендикулярен этой касательной.
То есть угол ОВА=90°, а ∆ОВА – прямоугольный.
В прямоугольном ∆ВАО:
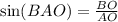
Подставим известные значения:
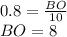
ВО – радиус окружности.
Диаметр вдвое больше радиуса, следовательно d=BO*2=8*2=16 см.
ответ: 16 см.
х+х+50=180
2х=180-50
2х=130
х=130:2
х=65
180-65=115