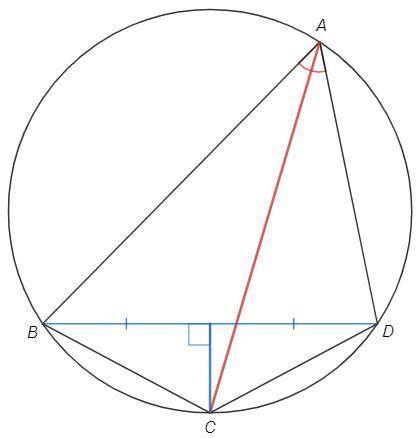
Рассмотрим △BAD.
Дано, что точка С лежит на биссектрисе угла A и серединном перпендикуляре к BD.
Биссектриса и серединный перпендикуляр пересекаются на описанной окружности △BAD (делят дугу BD пополам).
Таким образом, если биссектриса и серединный перпендикуляр НЕ СОВПАДАЮТ, но пересекаются, то точка С лежит на описанной окружности △BAD.
Биссектриса и серединный перпендикуляр не совпадают, если △BAD не равнобедренный (BD - основание).
Достаточные условия:
AB≠AD.
∠BCA>90 (тогда BD не перпендикулярен AC).
BD не перпендикулярен AC.
∠ABC≠∠ADC (тогда ABD≠ADB).
∠BCA≠∠ACD (тогда CA не биссектриса в BCD, следовательно не серединный перпендикуляр).
Объяснение:
d₁-d₂=14
d₁=14+d₂
Діагоналі у точці перетину діляться навпіл і утворюють прямокутні трикутники.Катети дорівнюють половинам діагоналей: 14+d₂ / 2 та d₂/2.
За теоремою Піфагора:
17²=(14+d₂ /2)²+ (d₂/2)²
289=(14+d₂)² /4+d₂²/4
289*4=(14+d₂)² +d₂²
1156=14²+28d₂+d₂²+d₂²
2d₂²+28d₂-960=0 :2
d₂²+14d₂-480=0
D = b² - 4ac = 14² - 4·1·(-480) = 196 + 1920 = 2116
x₁ = -14 - √2116 /2·1 = -14 - 46/ 2 = -60 /2 = -30 не підходить
x₂ = -14 + √2116/ 2·1 = -14 + 46 /2 = 32/ 2 = 16 см -d₂
d₁=16+14 = 30 см
S=1/2× 16×30=240 см²