Вравнобедренном треугольнике авс с прямым углом с проведены биссектрисы ам и bn,пересекающиеся в точке о.найдите величину угла аов(в граусах) нужно решение.

👇

Ответ:

Serdechkiцветочек

28.05.2023

Поскольку треугольник АВС прямоугольный и равнобедренный,

углы при основании АВ равны 90:2=45 градусов каждый.

Биссектрисы делят их пополам, и углы при основании АВ треугольника АОВ равны половине 45 градусов, а их сумма равна 45 градусам.

Так как сумма углов треугольника 180 градусов. угол

АОВ равен

180-45=135 градусам.

Вравнобедренном треугольнике авс с прямым углом с проведены биссектрисы ам и bn,пересекающиеся в точ

4,5(93 оценок)

Открыть все ответы

Ответ:

kozarmarjna15

28.05.2023

Из нового синтетического материала изготовили брусок в форме прямоугольного параллелепипеда, полная поверхность которого равна 192 см2.

Брусок был подвергнут давлению по всем граням таким образом, что форма прямоугольного параллелепипеда сохранилась, но каждое ребро уменьшилось на 1 см.

Сравнивая два бруска, имеющих форму прямоугольного параллелепипеда, установили, что длина, ширина и высота второго бруска соответственно на 1 см больше, чем у первого бруска, а объем и полная поверхность второго бруска соответственно на 18 см3 и 30 см2 больше, чем у первого.

Одно из боковых ребер наклонного параллелепипеда составляет равные острые углы с прилежащими к нему сторонами нижнего основания.

Через диагональ нижнего основания произвольного параллелепипеда и середину не пересекающего ее бокового ребра проведена плоскость.

Как относятся объемы образовавшихся при этом частей параллелепипеда?

Дан параллелепипед ^SCDA^jCjDj.

Доказать, что в прямоугольном параллелепипеде ABCDA1B1C1D1 сумма.

1) Пусть Xf, хг и х3 — длины ребер, выходящих из одной вершины некоторого прямоугольного параллелепипеда.

2) Найти длины ребер такого прямоугольного параллелепипеда, у которого сумма всех ребер, полная поверхность и объем соответственно равны 48 см, 88 см2 и 48 см9.

Длины ребер, исходящих из общей вершины некоторого прямоугольного параллелепипеда, являются корнями уравнения а*3+ ~\-bx*-\-cx-}-d=Q.

Определить длину диагонали этого параллелепипеда.

Найти площадь поверхности сферы, описанной около прямоугольного параллелепипеда, три измерения которого являются корнями уравнения Х3+шг2+йлг+с=0.

] Доказать, что сумма квадратов длин всех ребер параллелепипеда равна сумме квадратов длин всех его четырех диагоналей.

Доказать, что из всех прямоугольных параллелепипедов С данной суммой всех ребер наибольший объем имеет куб.

Диагональ прямоугольного параллелепипеда рагаа 13 см, _а диагонали его боковых граней равны 4У10 см и 3]/17 см.

В прямом параллелепипеде стороны основания равны а и Ь, острый угол между ними содержит 60°.

Большая диагональ основания конгруэнтна меньшей диагонали параллелепипеда.

Основанием прямого параллелепипеда служит ромб.

В основании прямого параллелепипеда лежит параллелограмм со сторонами 1 см и 4 см и острым углом 60°.

Основанием параллелепипеда служит квадрат.

Определить полную поверхность этого параллелепипеда.

Определить объем прямоугольного параллелепипеда, диагональ которого равна / и составляет о одной гранью угол 30°, а с другой 45°.

Основанием прямого параллелепипеда служит ромб, площадь которого равна Q.

Стороны основания прямоугольного параллелепипеда равны а и Ь.

Стороны основания прямоугольного параллелепипеда равны а и Ь.

Определить объем прямоугольного параллелепипеда, если его диагональ равна d, а длины ребер относятся, как т: п: р.

В прямом параллелепипеде стороны основания равны а и Ь и образуют угол 30°.

Стороны основания прямоугольного параллелепипеда относятся, как т: п, а диагональное сечение представляет собой квадрат с площадью, равной Q.

Измерения прямоугольного параллелепипеда равны 2 см, 3 см и 6 см.

Из медной болванки, имеющей форму пря--моугольного параллелепипеда размером 80 смХ20 смХ Х5 см, прокатывается лист толщиной 1 мм.

В наклонном параллелепипеде проекция бокового ребра на плоскость основания равна 5 дм, а высота равна 12 дм.

Основанием параллелепипеда служит ромб со стороной а и острым углом 30

4,4(40 оценок)

Ответ:

татьяна1019

28.05.2023

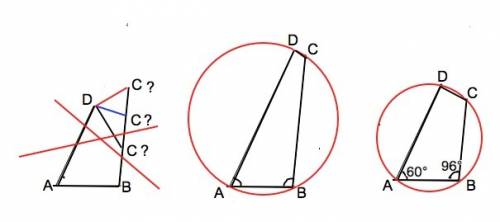
Задача имеет решение только если АВСD – четырехугольник, вписанный в окружность. (см. рисунки вложения)

В противном случае величину углов АDC и DCB вычислить невозможно, они могут принимать различное значения, лишь бы их сумма была равна разности между суммой углов четырехугольника и суммой углов АВС и BAD, т.е. 204°

-----------

Четырехугольник можно вписать в окружность, если сумма его противолежащих углов равна 180º.

Тогда ∠ADC=180°-∠ABC=180°-96=84°

∠BCD=180°-∠BAD=180°-60°=120°⇒

∠BCD-∠ADC=120°-84°=36°.