Доказательство в объяснении.
Объяснение:
Определение: внешний угол треугольника (многоугольника) - угол, образованный одной из его сторон и продолжением смежной стороны.
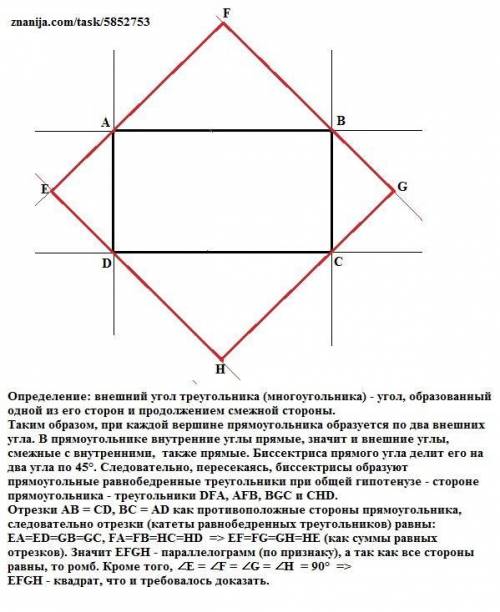
Таким образом, при каждой вершине прямоугольника образуется по два внешних угла. В прямоугольнике внутренние углы прямые, значит и внешние углы, смежные с внутренними, также прямые. Биссектриса прямого угла делит его на два угла по 45°. Следовательно, пересекаясь, биссектрисы образуют прямоугольные равнобедренные треугольники при общей гипотенузе - стороне прямоугольника - треугольники DFA, AFB, BGC и CHD.
Отрезки АВ = CD, BC = AD как противоположные стороны прямоугольника, следовательно отрезки (катеты равнобедренных треугольников) равны: EA=ED=GB=GC, FA=FB=HC=HD => EF=FG=GH=HE (как суммы равных отрезков). Значит EFGH - параллелограмм (по признаку), а так как все стороны равны, то ромб. Кроме того, ∠E = ∠F = ∠G = ∠H = 90° =>
EFGH - квадрат, что и требовалось доказать.
Пусть ABCD - равнобочная трапеция, AB||CD, BC=AD, AB<CD
Углы при основании равнобочной трапеции равны
угол А=угол В, угол С=угол D
Сумма углов при боковой стороне равна 180 градусов
угол А+угол D=180 градусов
угол В+угол С=180 градусов
по условию угол А:угол С=4:5
Пусть угол С=5х, тогда угол А=4х
отсюда
угол А+угол С=180 градусов
4х+5х=180 градусов
9х=180 градусов
х=180 градусов:9=20 градусов
4х=4*20=80 градусов
5х=5*20=100 градусов
меньший угол равен 80 градусов