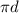. Так как по условию С=7
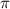, то d=7, а значит медиана равна 3,5.
СА – касательная к окружности. Вычислите градусную меру угла АВО, если ∠ВАС=58°.
[3]
2. Равнобедренный треугольник АВС (АВ=ВС) вписан в окружность с центром в точке О. Найдите величины дуг АС, АВ и ВС, если ∠АОС=70°. [4]
3. В окружности с центром в точке О проведен диаметр РМ=16,8 см и хорда АК, перпендикулярная РМ и равная радиусу данной окружности. Диаметр РМ и хорда АК пересекаются в точке Е.
a) выполните чертеж по условию задачи;
b) найдите радиус окружности; [4]
c) найдите длину отрезка АЕ;
d) вычислите периметр треугольника АОК.
4. В прямоугольном треугольнике СОК ( О = 90°) , СК= 18, СКО = 30° с центром в точке С проведена окружность. Каким должен быть ее радиус, чтобы:
а) окружность касалась прямой КО; [4]
b) окружность не имела общих точек с прямой КО;
c) окружность имела две общие точки с прямой КО?
5. Постройте треугольник АМР по сторонам АM=7 см, МK=6 см и углу ∠АМР = 45о. В полученном треугольнике постройте серединный перпендикуляр к стороне АР
Объяснение:
Определение: Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла.
Вертикальные углы равны.
----------------
При пересечении двух прямых получаются 4 угла. Углы с общей стороной, у которых две другие составляют прямую линию, называются смежными. Их сумма равна величине развёрнутого угла, т.е. 180°
Таких пар получается 4:
1) ∠ВОС+∠СОД=180°
2) ∠ДОА+∠СОД=180°
Суммы двух слагаемых равны, причем в каждой одно из слагаемых - одно и то же.Значит, вторые слагаемые тоже равны.
Вертикальные ∠ ВОС =∠ДОА
Аналогично
3) ∠ДОА+∠АОВ=180°
4) ∠ВОС+∠АОВ=180° ⇒
Вертикальные∠АОВ=∠ДОС
Доказано равенство вертикальных углов. .