1)Подобие треугольников АВС и ВСД. Углы АВС и ВДС - прямые. Углы ВАС и ДВС равны, т.к. ВАС=180-(90+ВСА) и ДВС=180-(90+ВСД). косинус ДВС=СД / ВД = 18/24=0,75. Значит, и косинус ВАС тоже равен 0,75.
2)sin 37=CD:AC
cos 37=AD:AC
S=AD*CD
CD=3*sin37
AD=3*cos37
S=AD*CD=9sin37*cos37=4,32 см^2
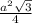, тогда площадь ромба будет равна 2*(4²√3/4)=2*4*√3=8√3
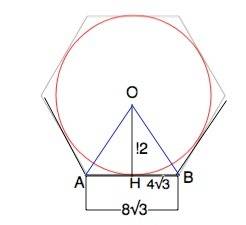
Центр вписанной в угол окружности лежит на биссектрисе. Окружности, вписанной в правильный многоугольник - в точке пересечения биссектрис его углов.
На рисунке приложения АВ - сторона, АО=ВО - биссектрисы углов правильного многоугольника. ОН - радиус вписанной окружности,
tg∠ОВН=ОН:ВН=√3. ⇒ Угол ОВН=60°, угол многоугольника 120°, смежный с ним внешний угол равен 60°.
Сумма внешних углов многоугольника 360°. Количество внешних углов, взятых по одному при вершинах, равно числу сторон многоугольника.
Число сторон 360°:60°=6.
Радиус описанной около правильного шестиугольника окружности равен его стороне.
R=8√3
C=2πR=16√3π
1
Одна из формул, которая используеться, если у нас есть прямокуугольник с высотой, опущеной до гипотенузы:
Тепер рассматриваем прямоугольник ABD, за теоремой пифагора находим AB:
Из этого же треугольника находим синус Альфа. Синус - отношение прилягающего катета к гипотенузе.
2
Одна сторона равна 8*sin(37 градусов), другая 8*cos(37 градусов).
Площадь равна 8*sin(37 градусов)*8*cos(37 градусов)=32*2*sin(37 градусов)*cos(37 градусов)=
=32*sin(74 град)=32*0,961=30,76 см^2