а) В правильном треугольнике центры вписанной и описанной окружностей - точка пересечения медиан (биссектрис, высот, так как они совпадают).
Медианы точкой пересечения делятся в отношении 2 : 1, считая от вершины. При этом больший отрезок высоты является радиусом описанной окружности, а меньший - вписанной.
r = h/3
R = 2h/3
б) Формулы, связывающие сторону правильного многоугольника с радиусами вписанной и описанной окружностей:
a(n) = 2r · tg(180°/n)
a(n) = 2R · sin(180°/n)
где a(n) - сторона правильного многоугольника, n - количество его сторон.
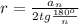
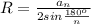
n = 5
r = a / (2tg36°)
R = a / (2sin36°)
в) n = 6
r = a / (2tg30°) = a√3/2
R = a / (2 sin30°) = a /(2 · 1/2) = a
33,88
Объяснение:
1) По формуле Герона находим площадь треугольника:
S = √(p · (p-a)·(p-b)·(p-c)),
где p - полупериметр треугольника:
р = P/2 = (17+65+80)/2 = 162:2=81
S = √(81 · (81-17)·(81-65)·(81-80)) = √(81 · 64 · 16 · 1) = √82944 = 288.
2) S = (17·h₁)2 = (65· h₂)/2 = (80· h₃)/2,
где h₁, h₂ и h₃ - высоты, проведённые к соответствующим сторонам треугольника;
следовательно,
2S = 17·h₁ = 65· h₂ = 80· h₃.
Очевидно, что наибольшая высота проведена к наименьшей стороне:
2· 288 = 17·h₁,
откуда h₁ = 576 : 17 ≈ 33,88.
ответ: 33,88.