
ответ: 16√2
Объяснение:
Сумма углов трапеции, прилежащих к одной боковой стороне, равна 180°.
∠BCD + ∠CDA = 180°
∠CDA = 180° - ∠BCD = 180° - 150° = 30°
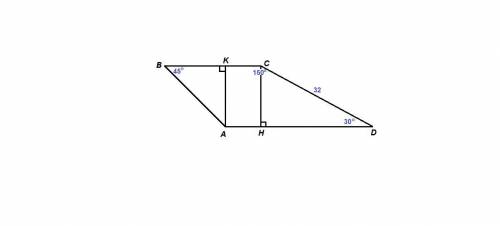
Проведем высоты СН и АК.
ΔCHD: ∠CHD = 90°,
СН = 1/2 CD = 1/2 · 32 = 16, по свойству катета, лежащего против угла в 30°.
АК = СН = 16 как высоты трапеции.
ΔАВК: ∠АКВ = 90°,
∠ВАК = 90° - ∠АВК = 45°, так как сумма острых углов прямоугольного треугольника равна 90°.
∠АВК = ∠ВАК = 45°, ⇒ ΔАВК равнобедренный, значит
ВК = АК = 16.
По теореме Пифагора:
АВ = √(АК² + ВК²) = √(16² + 16² ) = √(16² · 2) = 16√2
Верно
2)Центр окружности, описанной около произвольного треугольника, лежит в точке пересечения медиан
Не верно
3)Центр вписанной в треугольник окружности лежит в точке пересечения биссектрис треугольника
Верно
4)В любой треугольник можно вписать окружность
Верно
5)Центр окружности, описанной около прямоугольного треугольника, лежит в вершине прямого угла
Не верно
6)Около любого треугольника можно описать окружность
Верно
7)Центр описанной около произвольного треугольника окружности лежит в точке пересечения высот треугольника
Не верно