ПУсть АВс - данный треугольник, вн.угол А=140 градусов, угол С=38 градусов
Внешний угол и внутренний смежные, поэтому их сумма равна 180 градусов
угол А=180 градусов-внешн. угол А=180 градусов-140 градусов=40 градусов
Сумма углов треугольника равна 180 градусов
уго лА+угол В+угол С=180 градусов
угол В=180 градусов-угол А-угол С=180 градусов-40 градусов-38 градусов=102 градуса
ответ: 102 градусов, 40 градусов
Прямоугольный треугольник, следовательно, один из углов будет равен 90 градусам. Острые углы равны = 180 - 90 ( прямоугольный угол )
Теперь решаем через уравнение :
Пускай один из углов будет равен x , а второй x+6
Тогда получим уравнение: x + (x+6)= 90
Раскрываем скобки: x+x+6=90
2x= 90-6
2x=84
x=42 ( один из острых углов)
Теперь подставим в выражение x+6 ( второй острый угол) и получим
42+6 = 48
ответ: Остр.угол 1 = 42 Остр.угол 2= 48
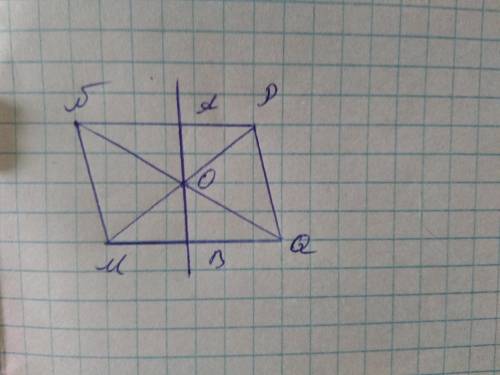
а) Рассмотрим ΔMBO и ΔAPO
1) ∠AOP=∠MOB - как вертикальные углы
2) ∠OMB=∠APO - как накрест лежащие углы при параллельных прямых NP и MQ и секущей MP. (NP//MQ - по определению параллелограмма)
3) MO=OP - по свойству параллелограмма (точкой пересечения делит диагонали пополам)
Значит ΔMBO и ΔAPO равны по двум углам и стороной между ними. Следовательно AO=OB - как соответственно равные элементы в равных треугольниках.
б) 1) Из пункта а) ΔMBO = ΔAPO, значит MB=AP=2 см - как соответственно равные элементы в равных треугольниках.
2) NP=NA+AP=3+2=5см
Объяснение:
38 гр первый угол треугольника
180-140=40 гр второй угол треугольника
180-(40+38)=102 гр третий угол треугольника