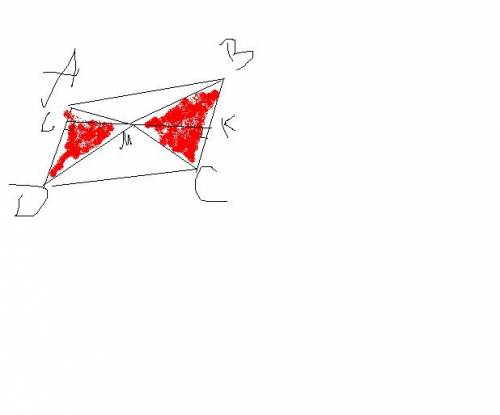
проведем через точку М, пряммую перпендикулярную АD, так как AD||BC, то она будет перпендикулярна и прямой ВС, пусть пряммую AD она пересекает в точке L, а пряммую BC в точке K.
Тогда LM - высота параллелограмма ABCD, LM - высота треугольника ADM, KM - высота треугольника BCM.
Площадь парарлелограмма равна произведению его стороны на высоту, проведенную к этой стороне
Площадь треугольника равна половине произведения стороны на высоту провдеенной к этой стороне
Поэтому
S(AMD)+S(BMC)=1/2*AD*LM+1/2*BC*KM=так противоположные стороны парарлелограмма равны=
=1/2*AD*LM+1/2*AD*KM=1/2*AD*(LM+KM)=1/2*AD*LK=1/2*S(ABCD), что и требовалось доказать
Свойство --- это характеристика известного объекта
(например, если дан ромб, то из этого следует,
что его диагонали взаимно перпендикулярны)))
а признак --- это характеристика неизвестного объекта, т.е.
необходимо определить что это за объект (по признакам)))
т.е. если сказано, что диагонали 4-угольника взаимно перпендикулярны,
то из этого не следует, что это ромб (это НЕ признак)))
если стороны 4-угольника равны, то точно ничего утверждать нельзя
--- может быть это ромб, а может быть это квадрат --- это НЕ признак))
а вот если известно, что это квадрат,
то точно у него стороны равны (это свойство)))
если известно, что это ромб,
то точно у него стороны равны (это свойство)))
если диагонали 4-угольника точкой пересечения делятся пополам,
то это точно параллелограмм (это ПРИЗНАК)))
это может быть и прямоугольник, это может быть и ромб
(они же все являются параллелограммами)))
дан треугольник (какой-то, не известно какой),
но про него известно, что две стороны у него равны (это ПРИЗНАК)
---вывод: это точно равнобедренный треугольник
дан равнобедренный треугольник (известно какой)
---вывод: у него две стороны точно равны (это СВОЙСТВО)
-3
Объяснение:
угловой коэффициент он же tg угла наклона прямой производной от заданной функции
y' = -3