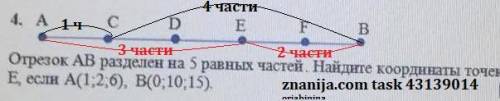
Отрезок АВ разделён на 5 равных частей. Найдите координаты точек С и Е, если А ( 1; 2; 6), В(0; 10; 15) .
Объяснение:
1) Для точки С имеем λ= 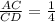 =0,25 .
=0,25 .
x(C)= 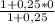 =1:1,25=0,8 ,
=1:1,25=0,8 ,
у(C)= 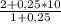 =4,5:1,25=3,6 ,
=4,5:1,25=3,6 ,
z(C)= 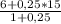 =9,75:1,25=76,8 . Значит С( 0,25 ; 3,6 ; 7,8)
=9,75:1,25=76,8 . Значит С( 0,25 ; 3,6 ; 7,8)
2) Для точки Е имеем λ= 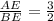 =1,5 .
=1,5 .
x(E)= 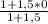 =1: 2,5=0,4 , у(E)=
=1: 2,5=0,4 , у(E)= 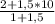 =17 : 2,5=6,8
=17 : 2,5=6,8
z(E)= 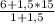 =9,75: 2,5=11,4 Значит С( 0,4 ; 6,8 ; 11,4) .
=9,75: 2,5=11,4 Значит С( 0,4 ; 6,8 ; 11,4) .
========================
х=(х₁+λх₂):(1+λ) ,у=( у₁+λу₂):(1+λ) ,где (х₁;у₁), (х₂;у ₂) -координаты концов отрезка , (х;у)-координаты точки, делящей отрезок в заданном отношении.
Объяснение:
Объем пирамиды вычисляется по формуле 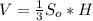 , где
, где 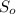 - площадь основы. Пирамида правильная, значит AB = BC = CD = DA = a - сторона основы, а основа - квадрат, значит
- площадь основы. Пирамида правильная, значит AB = BC = CD = DA = a - сторона основы, а основа - квадрат, значит 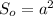 .
.
===================
Сперва можем найти высоту.
Из прямоугольного ΔASO по соотношениям найдем катет. Знаем гипотенузу и противолежащий катет, а значит:
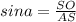 =>
=> 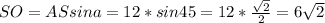 .
.
===================
Теперь нужно найти площадь основы 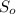 , сделать это можно с диагоналей. Диагональ можно найти опять же из треугольника ASO.
, сделать это можно с диагоналей. Диагональ можно найти опять же из треугольника ASO.
Соотношение прилежащего катета и гипотенузы: 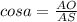 =>
=> 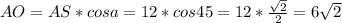 - только половина диагонали квадрата; вся диагональ:
- только половина диагонали квадрата; вся диагональ: 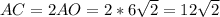 .
.
Есть формула диагонали квадрата: 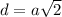 , из неё выразим сторону =>
, из неё выразим сторону => 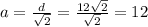 - сторона основы.
- сторона основы.
Найдем площадь основы 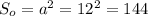 ед.²
ед.²
===================
Теперь можем найти объем пирамиды:
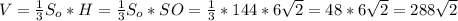 ед.³
ед.³
Площадь боковой поверхности правильной пирамиды равна сумме площадей ее боковых граней, равных между собой.
Площадь одной боковой грани - площадь равнобедренного треугольника,
т.е. половина произведения апофемы на сторону основания пирамиды.
См. рисунок:
S бок= 3 SᐃAKB= 3 KH*AB:2
Основание О высоты КО правильной пирамиды находится в точке пересечения высот её основания ( центре вписанной окружности).
Этот центр делит высоту основания СН в отношении 2:1, считая от вершины треугольника ( по свойству медиан, которые в правильном треугольнике и высоты, и биссектрисы).
Итак, ОН=ОС:2.
ОС=√(КС²-ОК²)=√(25-13)=2√3 см
ОН=√3 см
Апофема
КН=√(КО²+ОН²)=√(13+3)=4 см
АВ=АС=ВС=СН:sin(60°)
СН=ОН+ОС=3√3
АВ=2*(3√3):√3=6 см
S бок=0,5*KH*AB=2*3*6=36 см²