Примем боковые стороны , равными а, основание b, медиана m.
Периметры равны: 21 = a + 0,5a + m = 1.5a + m.
12 = m + 0,5a + b.
Вычтем из первого уравнения второе: a - b = 9.
Сторону b заменим: b = a - 9.
Находим длину медианы m = AD для равнобедренного треугольника.
m = (√(2b² + a²))/2 = (√(2(a - 9)² + a²))/2 = (√(2a² - 36a + 162 + a²))/2 =
= (√(3a² - 36a + 162))/2.
Теперь используем полученное значение медианы для периметров треугольников.
21 = 1,5a + (√(3a² - 36a + 162))/2.
(2*21 - 2*1,5a)² = (√(3a² - 36a + 162))².
1764 - 252a + 9a² = 3a² - 36a + 162.
6a² - 216a + 1602 = 0. Сократим на 6.
a² - 36a + 267 = 0.
D=(-36)^2-4*1*267=1296-4*267=1296-1068=228;
Дискриминант больше 0, уравнение имеет 2 корня:
a_1=(√228-(-36))/(2*1)=(√228+36)/2=√57+36/2=√57+18~~25.5498;
a_2=(-√228-(-36))/(2*1)=(-√228+36)/2=-√57+36/2=-√57+18~~10.45017.
Первый корень не принимаем - не соответствует условиям.
ответ: 2 стороны по 18 - √57, третья равна 9 - √57.
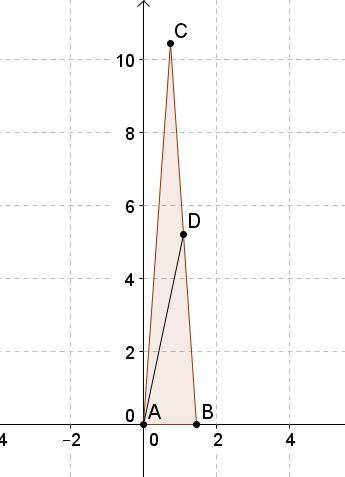
см. рисунок во вкладке
Объем конуса V=1/3*pi*r^2*h (1)
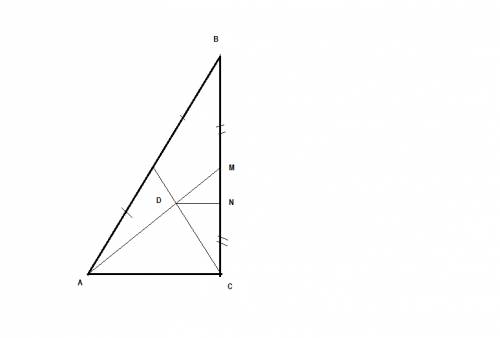
Пусть конус образован вращением треугольника АВС вокруг катета ВС,
тогда радиус основания АС=r ; высота BC=h.
По условию 1/2*rh=S подставим в (1)
V= (2pi/3*r) * (1/2*rh)=2pi/3*r*S. (2)
Кроме того , по условию , 2pi*DN=L , где D- точка пересечения медиан, a DN перпендикуляр к ВС.
Но DN : AC =DM : AM = 1:3 (на основании свойства медиан)
откуда DN=r/3 , следовательно L=2pi/3*r , отсюда r=3L/2pi. (3)
Подставим (3) в (2)
V=2pi/3*S*3L/2pi = SL
ответ V=SL
ответ: 28 см.
Объяснение:
"Площадь параллелограмма 12 см², острый угол равен 30°, одна из сторон параллелограмма равна 2 см. Найдите периметр параллелограмма."
***
Проведем высоту из точки В - ВЕ ⊥ AD.
BE/AB=Sin30*. BE=AB*(1/2)=2*1/2=1 см.
S=ah; a=S/h=12/1=12 см.
Р=2(a+b)=2(2+12)=2*14=28 см.