50
Объяснение:
1. Найдем длину диагоналей прямоугольника, лежащего в основании пирамиды. По теореме Пифагора:
дм.
AO = AC/2= 100/2 = 5 дм
2. Для наглядности, начертим сечение по плоскости на которой лежит треугольник AKC
По теореме Фалеса (при пересечении угла параллельными прямыми стороны угла делятся на пропорциональные отрезки) видно, что параллельные прямые AK и OM делят AC и KC на пропорциональные отрезки, так как AO=OC=AC/2 (точка O середина диагонали), верно равенство КМ=MC=KC/2.
Аналогично прямые КО и MN делят ONC на равные отрезки
ON=NC
По признаку равенства прямоугольных треугольников, ΔONM = ΔCNM
(по двум катетам).
Вычислим KC по теореме Пифагора:
Далее OM=MC=KC/2 =
Площадь равнобедренного треугольника BMD равна половине произведения основания BD на высоту OM
S BDM = BD*OM =
ответ: пәнінен 4-тоқсанға арналған жиынтық бағалаудың тапсырмалары
І нұсқа
1. KL – шеңбердің қанамасы. KOL үшбұрышының ОL қабырғасының ұзындығын табыңыз
ет
2. Шеңберге іштей ABC теңбүйірлі үшбұрышы сызылған. Үшбұрыштың AC табанының
ұзындығы шеңбердің радиусына тең. AC, AB және BC догаларының өлшемдерін анықтаңыз.
[4]
3. Шеңбер бойында сататын А нүктесі арқылы AB диаметрі мен AC хордасы жүргізілген. АС =6
және ZBAC =30°. AB диаметріне перпендикуляр CM хордасы кіргізілген және олар Кнүктесінде
Қиылысады. СМ хордасының ұзындығын табыңыз.
[5]
4. ABC тікбұрышты үшбұрышында (ZC = 90°) BC = 5, ZABC = 45°. Центрі А нүктесінде
болатындай шеңбер жүргізілген.
а) Шеңбер мен BC түзуі жанасу үшін;
Б) шеңбер мен BC түзуінің ортақ нүктелері болмауы үшін;
с) шеңбер мен BC түзуінің екі ортақ нүктесі болуы үшін шеңбердің радиусы қандай болуы тиіс?
5. Салу есебі:
a, b және с қабырғалары бойынша үшбұрыш салыңыз.
Объяснение:
Найдите отношение объёма октаэдра к объёму куба, вершинами которого являются центры граней октаэдра.
Объяснение:
1) Октаэдр это геометрическое тело из восьми граней, каждая их которых - правильный треугольник. Пусть ребро октаэдра а.
V( октаэдра)=1/3*√2*а³ , ABCD-квадрат .
2) Пусть Р-центр правильного ΔАВМ .Тогда М-точка пересечения медиан .Тогда по т. о точке пересечения медиан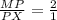 ⇒
⇒ 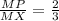 .
.
3) Аналогично для правильного ΔDCМ ⇒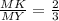 .
.
4) ΔМРК подобен ΔМXY по 2-м пропорциональным сторонам ( см п. 2,3) и равному углу между этими сторонами (∠РМК-общий).
Тогда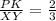 ,
, 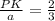 ,РК=
,РК= 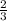 *а .
*а .
5) V( куба)=(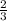 *а)³ =
*а)³ =  *а³ . Тогда отношение объёмов будет равно :
*а³ . Тогда отношение объёмов будет равно :