Квадрат вписан в окружность, которая, в свою очередь, вписана в правильный треугольник.
Пусть сторона треугольника равна а.
Высота его равна
(a√ 3):2
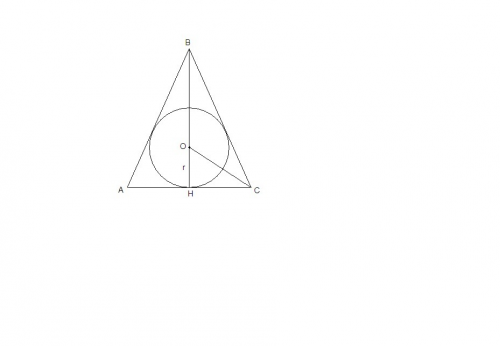
Радиус окружности, вписанной в правильный треугольник, равен одной трети ее высоты:
r=(a√ 3):6
Радиус описанной вокруг квадрата окружности равен половине его диагонали.
А диагональ = 2r.
Так как окружность одна и та же:
d=2r =2(a√ 3):6=(a√ 3):3
Пусть сторона квадрата равна у. Тогда его диагональ
d=у√2
Подставим значение диагонали
у√2=(a√ 3):3
у=(a√ 3):3):√2=(a√ 3):3√2
Сторона треугольника : сторона квадрата
а:у=а:(a√ 3):3√2=3а√2):a√ 3
Умножим на √ 3 числитель и знаменатель дроби:
а:у=3 √2): √ 3=3 √2*√ 3): √ 3*√ 3=3√6):3=√6
ответ: отношение сторон правильных треугольника и квадрата =√6:1 или
квадрата и треугольника 1:√6
найдем сторону ромба
AB^2=AO^2+OB^2=9+16=25(O- центр впис. окр. и точка пересечения диагоналей)
AB=5
Sabcd=1/2 * 6*8=24
найдем высоту треуг. COB - OK
Scob=1/2 * 3*4=6 OK=2S/CB=12/5
апофема MK^2=MO^2=OK^2=169/25 MK=13/5
Sбп=4(1/2 * MK*BC)=26
Sпп=26+24=50