Дано :
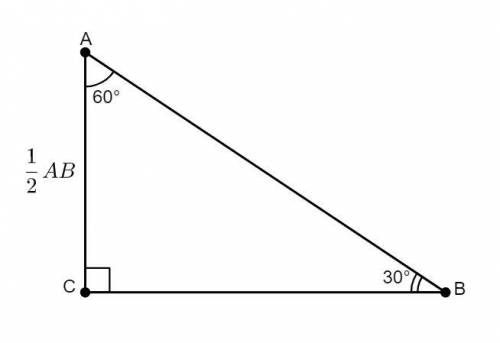
ΔАВС — прямоугольный (∠С = 90°).
∠А = 60°.
АВ + короткий катет = 9 см.
Найти :
∠В = ?
Короткий катет = ?
В прямоугольном треугольнике сумма острых углов равна 90°.Следовательно, ∠А + ∠В = 90° ⇒ ∠В = 90° - ∠А = 90° - 60° = 30°.
В треугольнике против меньшего угла лежит меньшая сторона.Так как ∠В — самый меньший угол в ΔАВС, то АС (катет, лежащий напротив этого угла) самая меньшая сторона, соответственно и есть короткий катет.
Тогда нам нужно найти АС.
В прямоугольном треугольнике против угла в 30° лежит катет, равный половине гипотенузы.Следовательно, АС =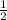 
*АВ или АВ = 2*АС.
Составим уравнение —
АВ + АС = 9 см
2*АС + АС = 9 см
3*АС = 9 см
АС = 3 см.
30° ; 3 см.
1в
2а
3б
4 г
Объяснение: