По рисунку определяем, что углы находим по функции arc tg по катетам.
Угол альфа = arc tg (3-1.5)/6 = arc tg(1/4).
Для элементов фурмы находим приращение высоты от 0 до 3-1,5 = 1,5.
Δ1 = 2*tgα = 2*(1/4) = 0,5.
Δ2 =4*tgα = 4*(1/4) = 1.
Δ3 = 6*tgα = 6*(1/4) = 1,5.
Высоты катетов:
h1 = 1,5+0.5 = 2 м.
h2 = 1,5+1 = 2,5 м.
h3 = 1,5+1.5 = 3 м.
Приводим значения углов:
α β γ θ
0,25 1 1,25 1,5 тангенс угла
0,24498 0,7854 0,8961 0,9828 радиан
14,0362 45 51,340 56,3099 градусов.
11.
Дано:
ΔАВС - равнобедренный
АС = ВС = 13
АВ = 10
Найти:
АС - высоту. опущенную на боковую сторону
СD - высота равнобедренного треугольника. опущенная на основание, является и медианой. Поэтому AD = BD = 0.5AB = 0.5 · 10 = 5.
По теореме Пифагора
АС² = CD² + AD²
13² = CD² + 5²
CD² = 13² - 5² = 144 = 12²
CD = 12
Площадь треугольника АВС
S = 0.5 CD · AB = 0.5 · 12 · 10 = 60
Площадь треугольника АВС можно также вычислить и так:
S = 0.5 BC · AE
откуда
АЕ = 2S : BC = 2 · 60 : 13 = 9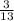 ≈ 9.23
≈ 9.23
АЕ = 9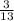 ≈ 9.23
≈ 9.23
12.
Дано:
MKNR - ромб
KR = 10 - 1-я диагональ ромба
MN = 12 - 2-я диагональ ромба
Найти:
МК - сторону ромба
Пусть О - точка пересечения диагоналей ромба.
Диагонали ромба делятся точкой пересечения пополам, поэтому
КО = 0,5 KR = 0.5 · 10 = 5
МО = 0,5 MN = 0.5 · 12 = 6
Диагонали ромба пересекаются под прямым углом, поэтому
КО ⊥ МО и ΔМКО - прямоугольный с гипотенузой МК.
По теореме Пифагора
МК² = КО² + МО²
МК² = 5² + 6² = 61
МК = √61 ≈ 7,81
Сторона ромба МК =√61 ≈ 7,81