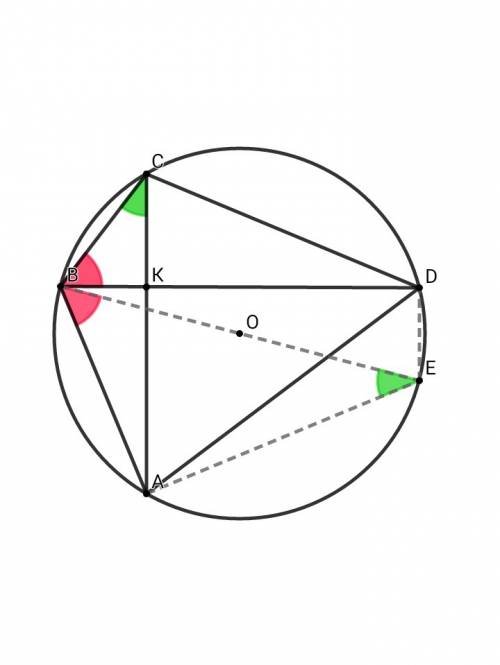
Проведём из точки D отрезок DE, параллельный диагонали АС, тогда ∠BDE = ∠BAE = 90° , BE - диаметр окружности ⇒ АСDE - равнобедренная трапеция ⇒ CD = AЕ
В ΔВАЕ по т. Пифагора: AB² + AE² = BE² ⇒ AB² + CD² = ( BK² + AK² ) + ( CK² + KD² ) = BE² = ( 2R )² = 4R²
Значит, BK² + AK² + CK² + KD² = 4R²
илиПостроим диаметр окружности ВЕ, тогда ∠ВАЕ = 90°
∠ВСА = ∠ВЕА - как вписанные углы, опирающиеся на общую дугу АВ
Из прямоугольных треугольников ВКС и ВАЕ следует, что ∠CBD = ∠ABE ⇒ CD = AE - как хорды, стягивающие равные дуги CD и АЕ
В ΔВАЕ по т. Пифагора: AB² + AE² = BE² ⇒ AB² + CD² = ( BK² + AK² ) + ( CK² + KD² ) = BE² = ( 2R )² = 4R²
Значит, BK² + AK² + CK² + KD² = 4R²
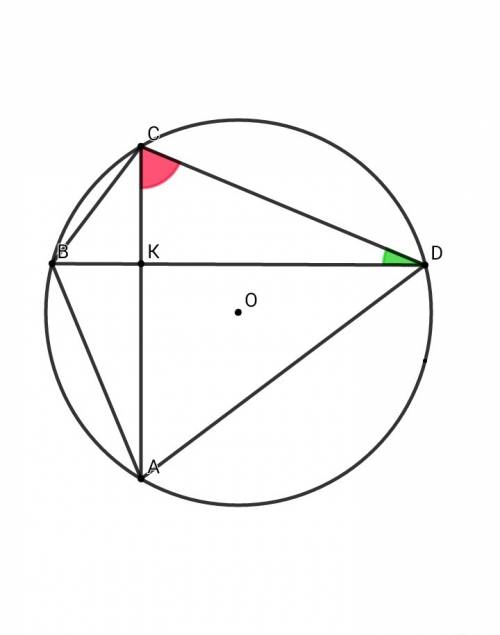
▪ Теорема синусовПусть ∠CDК = α , тогда ∠KCD = 90° - α
В ΔBCD по т. синусов: ВС/sinα = 2R ⇒ BC = 2R•sinα
В ΔACD по т. синусов: AD/sin( 90° - α ) = 2R ⇒ AD = 2R•cosα
BC² + AD² = ( 2R•sinα )² + ( 2R•cosα )² = 4R²•sin²α + 4R²•cos²α = 4R²•( sin²α + cos²α ) = 4R²
Значит, BK² + CK² + AK² + KD² = 4R²
Определение. Четырехугольником называется фигура, которая состоит из четырех точек и четырех отрезков, что последовательно их соединяют. При этом никакие три из данных точек не должны лежать на одной прямой, а отрезки, что их соединяют, не должны пересекаться. Точки называются вершинами четырехугольника, а отрезки, что их соединяют, - сторонами четырехугольника.
Определение. Вершины четырехугольника наиваються соседними, если они являются концами одной из его сторон.
Определение. Вершины четырехугольника, которые не являются соседними, называются противоположными.
Определение. Отрезки, которые соединяют противоположные вершины четырехугольника, называются диагоналями.
Определение. Стороны четырехугольника, которые выходят из одной вершины, называются соседними сторонами.
Определение. Стороны четырехугольника, которые не имеют общий конец, называются противоположными.
Четырехугольник помечают, записывая его вершины.
Определение. Периметром четырехугольника называется сумма длин его сторон.
Сумма углов четырехугольника равняется 360°.