60
Объяснение:
буду писать русским транслитом
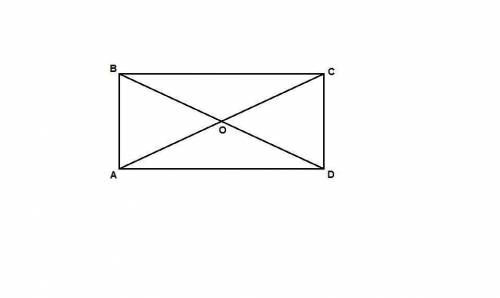
АБ = СД, ну, думаю понятно почему,
АС- гипотенуза треугольника БСД
гипотенуза равна 16, а катет 8, то есть гипотенуза в два раза больше катета, значит угол противоположный катету= 30
угол ДБС = 30, угол с = 90 по условию, а БДС = 180 - 90- 30 = 60, точно такая же схема с углом АСД, они оба равны 60, значит угол СОД = 180 - - 60 - 60 = 60
3) Дано:
АВCD - ромб,
AC и BD - диагонали ромба,
О - точка пересечения диагоналей,
угол BCD = 104*
Найти углы ABO.
Решение: возьмем произвольный ромб и обозначим его как ABCD, проведем в нем диагонали AC и BD. Они пересекутся в точке О. Известно также, что диагонали ромба перпендикулярны и делят его углы пополам. Тогда угол ВСО = углу ОСD = 104/2=51*. Рассмотрим один из получившихся треугольников - ВОС. В нем угол ВОС = 90* (так как диагонали ромба перпендикулярны). Угол ВСО = 51*, угол ВОС = 90*, значит угол ОВС = 180 - (51*+90*) = 39*. Но треуг. ВСО = треуг. АВО и значит все стороны и углы одного соответственно равны сторонам и углам другого. То есть в треугольнике АВО угол АВО = 39*, а угол ВОА = 90*.
60
Объяснение:
напротив большего угла лежит большая сторона, раз длина больше ширины в 2 раза то и угол будет больше в 2 раза. AOB и COD равны как вертикальные углы так и AOD и BOC равны . составляем уравнение 2х+2х+х+х=360 6х=360 х=60
нам нужно угол COD он у нас х так как меньше углов BOC и AOD в 2 раза, а х мы нашли 60