
Пусть D, E и F - точки касания вписанной окружности со сторонами треугольника АВС: АС, АВ и ВС соответственно.
Нам дано: АВ=30см, ВF=14см, FC=12см.
Заметим, что ВЕ=ВF=14см, DC=FC=12см, а АЕ=АD как касательные, проведенные из одной точки к окружности.
Тогда АЕ=АВ-ВЕ=30-14=16см, значит АD=16см. DC=FC=12см.
Значит АС=AD+DC=16+12=28см.
Полупериметр треугольника равен: р=(30+26+28):2=42см.
Есть формула для вписанной в треугольник окружности:
r=√[(p-a)(p-b)(p-c)/р], где р - полупериметр, а, b, c - стороны треугольника.
В нашем случае: r=√(12*16*14/42)=√64=8см.
ответ: r=8см.
Или по формуле r=S/p, где S - площадь треугольника.
Площадь найдем по формуле Герона:
S=√[p(p-a)(p-b)(p-c)] или в нашем случае: S=√(42*12*16*14)=√(6*7*2*6*16*2*7)=6*7*2*4=336см².
r=336/42=8см.
ответ: r=8см.
1. Равные многоугольники имеют равные площади (аксиома площадей).
Отсюда —
Равные четырёхугольники равновелики (равные по площади).
2. Обратное утверждение : "Если у четырёхугольников равные площади, то они равны".
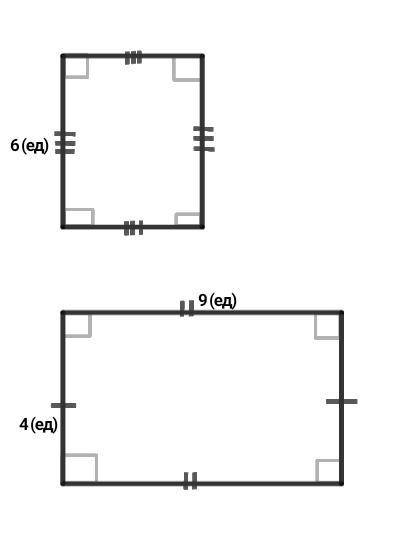
Рассмотрим квадрат со стороной 6 (ед) и прямоугольник с смежными сторонами, равными 9 (ед) и 4 (ед).
Логично, что эти фигуры не могут быть равными между собой, ведь у равных четырёхугольников равны все соответствующие элементы (у квадрата все стороны равны по 6 (ед), а у прямоугольника стороны попарно равны по 9 (ед) и 4 (ед), тоесть они никак не могут быть равными).
Однако же —
Площадь квадрата = квадрат стороны = (6 (ед))² = 36 (ед²).
Площадь прямоугольника = произведение смежных сторон = 9 (ед)*4 (ед) = 36 (ед²).
Мы доказали, что квадрат и прямоугольник не равны, однако имеют равные площади.
Поэтому обратное утверждение не всегда верно (верно только тогда, когда четырёхугольник равны).
1) Нет
2) Да
3) Да
4) Нет
5) Да
6) Да
7) Нет
8) Да
9) Нет