1) ∠BAD - ?
Рассмотрим ΔBAD
BA=AD=BD ⇒ ΔBAD - равносторонний
Т.к. Δ BAD равносторонний ⇒ все углы треугольника равны 60°
∠BAD = 60°
2) ∠ADC - ?
∠ADC состоит из углов ∠BDA и ∠CDB
ΔBAD и ΔBСD - равносторонние, т.к. все стороны равны
Из этого следует,что ∠BDA = ∠CDB = 60°
∠ADC = ∠BDA + ∠CDB = 60° + 60° = 120°
3) ∠DCB - ?
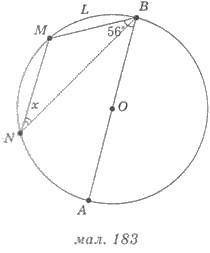
Векторы DA и CD не выходят из одной точки
Параллельным переносом делаем из вектора DА вектор CB
Рассмотрим ΔBCD
ΔBCD- равносторонний, т.к. все стороны равны
Т.к. Δ BAD равносторонний ⇒ все углы треугольника равны 60°
∠DCB = 60°
При решении задачи, как обычно. желателен рисунок.
Опустим из вершин тупых углов трапеции высоты к большему основанию.
Часть большего основания и высота, как катеты, и боковая сторона - гипотенуза, образовали прямоугольный треугольник из тех, что называют египетскими. Стороны в нем относятся как 3:4:5. Поэтому без вычислений ( хотя можно и теорему Пифагора применить) можно определить, что
меньший катет этого треугольника кратен 3. А так как боковая сторона вдвое больше 5,то и катет НD вдвое больше трех и
равен 6 см. Это - проекция боковой стороны на большее основание.
Точно так же с другой стороны от большего основания отсекается высотой отрезок, равный 6 см.
Так как большее основание равно 17, то средняя его часть равна
17-6*2=5 см
Эта часть является стороной прямоугольника, равной меньшему основанию.
ВС=5 см
Осталась арифметика:
Периметр трапеции равен 5+17+2*10=42 см