По условию ∆ АВС – равнобедренный, АВ = ВС → СК : ВК = АМ : ВМ = 5 : 8
Значит, CK = АМ = 5х , ВК = ВМ = 8х
ВМ = ВК = 8х , АМ = АЕ = 5х , СК = СЕ = 5х – как отрезки касательных к окружности
AB + BC + AC = P abc
8x + 5x + 8x + 5x + 5x + 5x = 72
36x = 72
x = 2
Из этого следует, что ВМ = ВК = 16 , АМ = АЕ = 10 , СК = СЕ = 10 → АВ = ВС = 26 , АС = 20
Рассмотрим ∆ АВЕ (угол АЕВ = 90°):
По теореме Пифагора:
АВ² = АЕ² + ВЕ²
ВЕ² = 26² – 10² = 676 – 100 = 576
ВЕ = 24
S abc =( 1/2 ) × AC × BE = ( 1/2 ) × 20 × 24 = 240
ОТВЕТ: S abc = 240
Объяснение:
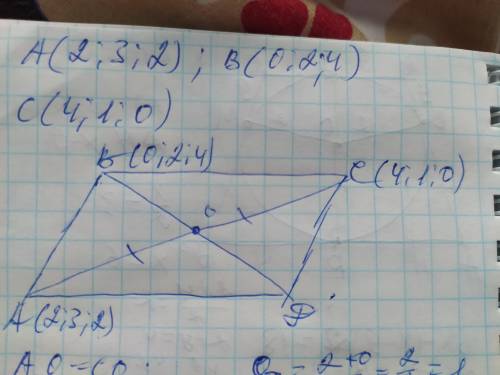
ответ: Д(6; 2; -1)
Объяснение: найдём координаты точки О - середины диагонали АС по формуле: Ох=(Ах+Сх)/2; Оу=(Ау+Су)/2;
Oz=(Аz+Cz)/2. Подставим данные координаты а формулу:
Ox=(2+4)/2=6÷2=3
Оу=(3+1)/2=4÷2=2
Оz=(2+0)/2=2/2=1
Итак: координаты О(3; 2; 1)
Так как координаты середины диагонали АС совпадает с серединой диагонали ВД, то:
Ох=(Ах+Дх)/2. Оу=(Ву+Ду)/2
3=(0+Дх)/2. 2=(2+Ду)/2
Дх=3×2. 2+Ду=2×2
Дх=6. Ду=4-2
Ду=2
Oz=(Bz+Дz)/2
1=(4+Дz)/2
4+Дz=2×1
Дz=3-4
Дz= -1
Координаты Д(6; 2; -1)
Нужно обозначить току О (пусть это будет точка на плоскости бетта, образованная пересекающимся лучом из точки А). Иными словами у нас будет АО (расстояние от А до бетта). АО=2 (по условию).
Теперь проводеем луч из точки А до линии, образованной пересекающимися плоскостями алья и бетта, пусть луч этот пересекается в точке В.
Теперь у нас есть треугольник АОВ. угол АОВ=90 градусов, т.к. плоскости наклонены под улом 45, то угол ОВА=45 градусов, значит, и второй угол тоже 45 градусов, а это значит, что весь треугольние АОВ мало того, что прямоугольный, так еще и равнобедренный. В этом треугольнике АО и ОВ - катеты, а АВ - гипотенуза.
АО=OВ=2
а АВ по теореме Пифагора
АВ^2=AO^2+OB^2
AB=корень квадратный из 8