
Находим координаты точки А как точки пересечения двух заданных сторон треугольника.
2х+у-1 = 0
4х-у-11=0, сложим уравнения: 6х - 12 = 0, отсюда х = 12/6 = 2,
значение у = 1-2*2 = -3.
Точка А(2; -3), точка Р(1; 2).
Вектор АР = (1-2; 2-(-3)) = (-1; 5)
Перпендикулярный вектор имеет такие координаты, скалярное произведение которых на координаты вектора АР равны 0.
Это будет вектор ВС(5; 1).
Теперь можно составить уравнение ВС по направляющему вектору ВС и точке Р.
(х - 1)/5 = (у - 2)/1.
х - 1 = 5у - 10.
ответ: уравнение х - 5у + 9 = 0.
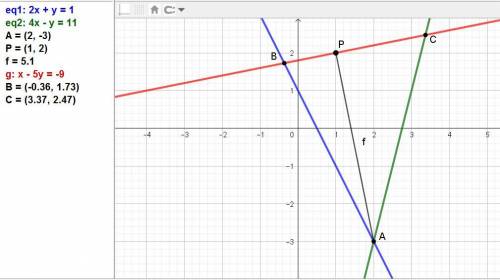
Угол ВСА = 45 градусов.
косинус угла 45 = АС : ВС ( прилежащий катет к гипотенузе )
косинус 45 = корень из 2 : 2
корень из 2 : 2 = АС : 10
АС = (10* корень из 2) : 2 = 5 корней из 2
По теореме Пифагора найдем ВА
ВА^2 = 100 - 50
ВА=корень из 50 = 5 корней из 2
Площадь прямоугольного треугольника равна 1/2 произведения катетов ( 1/2 *a*b )
ВА и АС - катеты, ВС - гипотенуза, значит
S = 1/2 * 5 корней из 2 * 5 корней из 2
S = 1/2 * 50 = 25.
( Если есть наименование (см,м,дм) , не забудь поставить квадрат! )