1.
а) По теореме пифагора — сумма квадратных катетов равна квадрату гипотенузы.
Если нам известна гипотенуза, и один из катетов, то формула такова: a^2+b^2 = c^2 => b^2 = c^2-a^2:
б) Гипотенуза равна 27 см, а один из катетов — 12см.
12^2см+b^2см = 27^2см
b^2 = 27^2-12^2
b^2 = 585
b = Корень из 585 — 24.186см.
2. Чтобы найти гипотенузу, опять используем теорему Пифагора: a^2+b^2 = c^2.
А тангенсы я не имею понятия, что такое.
б) 15^2+17^2 = c^2
225+289 = c^2
544 = c^2
c = Корень из 544 => c = 23.32см
Зная катеты, мы можем найти углы, лежащие против этих катетов, это как я помню - теорема косинусов: cos (α) =b^2+c^2−a^2/ 2bc (в картинке нагладнее представлено)
<α = 41^o
<β = 48.576^o
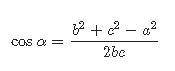
E∈ [AB] , F∈ [CD] ; M и N - точки пересечении средней линии EF с диагоналями AC и BD соответственно .
a) EM =NF =3 см или
b) MN =3 см .
ЕF - ?
обозн. AD =a ,BC =b.
EF =(a+b)/2 .
EM = NF =BC/2 =b/2 . Действительно EM и NF средние линии в треугольниках
ABC и BCD соответственно(средняя линия треугольника соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине ).
Аналогично из ΔABD : EN = AD/2 =a/2 * * * или из ΔACD : MF = AD/2=a/2 * * *
MN =EN - EM = a/2 -b/2 =(a-b)/2 .
а) b = 2*EM =2*3 см =6 см ;
EF =(a+b)/2 =(14 см+6 см)/2 =10 см .
b) MN =3 см.
MN =(a-b)/2 ⇒b =a -2MN ;
EF =(a+b)/2 =(a +a-2MN)/2 = a -MN =14 см -3 см = 11 см.
ответ : 10 см или 11 см.