Ребро не было указано в условии задачи, поэтому я обозначу его за {a}.
--------------
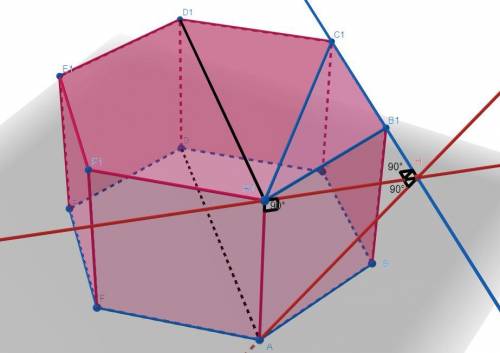
а)
проекция Точки A на плоскость (A1B1C1)=A1, проекция точки D=D1, значит проекция отрезка AD=A1D1.
Отрезок A1D1║B1C1 из свойств правильного шестиугольника, и A1D1║AD так как плоскость (ABC)║(A1B1C1) значит AD║B1C1 Ч.Т.Д.
---------------
б)
Рассмотрим треугольник A1B1C1, опустим высоту A1H на основание B1C1, AH Также будет ⊥B1C1 по теореме о трех перпендикулярах, значит AH искомое расстояние.
AA1 будет ⊥A1H так-как он ⊥ плоскости (A1B1C1).
найдем A1H методом площадей в треугольнике A1B1C1.

A1H также можно было найти рассмотрев треугольник A1BH, сказав что A1H=A1B1*sin(60)
-----------
теперь по теореме пифагора найдем AH:
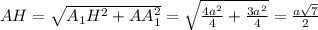
ответ: 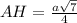
Дано:
вектор a =(9;-3)
вектор b =(-8;16)
вектор c = (?;?)
а) c = 2a+0,5b
b) c = 3a-b
а) c=2a+0,5b = (9×2;-3×2)+(0,5×(-8);0,5×16) = (18;-6)+(-4;8) = (14;2)
b) c=3a-b = (9×3;-3×3)-(-8;16) = (27;-9)-(-8;16) = (19; 7)
ответ: а) (14;2); b) (19;7).