Рассмотрим прямоугольный треугольник ABC (угол B - прямой, BO - медиана). Угол B опирается на дугу AB, а так как угол B - вписанный, то дуга AB равна 2*уголB = 180. Следовательно AC - диаметр, а центр AC - центр окружности. Но окружность так же проходит по точке B. А значит AO = OC = OB = r - радиус описанной окружности.
Доказано Надо доказать, что BO = AO = OC
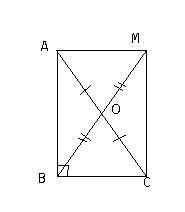
Рассмотрим прямоугольный треугольник ABC (угол B - прямой, BO - медиана). Продолжим BO, на линии отложим отрезок равный BO: OM (рисунок прилагается). Соединим точку M с точками A и C. Получится четырехугольник ABCM. Рассмотрим треугольники AOM и COB:
<AOM = <BOC (вертикальные углы)
AO = OC (О - середина AC)
BO = OM (по построению)
По 1 признаку равенства треугольников, ΔMOA = ΔBOC, следовательно все элементы в этих треугольниках равны:
АМ = BC; <MAC = <ACB - накрест лежащие углы. Так как накрест лежащие углы равны, то AM параллельно BC. По признаку параллелограмма (две противолежащие стороны равны и параллельны) четырехугольник ABCM является Параллелограммом. Но угол B - прямой, а значит параллелограмм является прямоугольником, а в прямоугольнике диагонали равны.
AC = BM - значит и их половины равны:
BO = AO = OC = OM
Что и требовалось доказать
1. Рассмотрим треугольники BMN и BAC.
<B общий, <BMN = <BAC, <BNM = <BCA (как соответственные углы, образованные при пересечении двух параллельных линий (MN и AC) третьей).
По третьей теореме подобия треугольников, ΔBMN подобен ΔBAC. Следовательно:
MN/AC = BM/AB
9/12 = BM/18
BM = 13,5
ответ: 13,5
2. cos<DAC = AD/AC
cos30° = 3/AC
√3/2 = 3/AC
AC = 6/√3 = 2√3
По теореме Пифагора:
AC² = AD² + DC²
(2√3)² = 9 + DC²
DC² = 12-9
DC² = 3
DC = √3
SΔ = AD*DC/2 = 3*√3/2 = 1,5√3
Проведем высоту DH. В прямоугольном треугольнике DHA:
sin<DAH = DH/DA
sin30° = DH/3
1/2 = DH/3
DH = 1,5
ответ: a)√3 и 2√3 б)1,5√3 в) 1,5