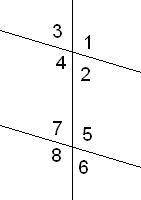
Определи взаимное расположение данной прямой и плоскости.
1. Прямая AA1 и плоскость (BCD): плоскость (BCD) это грань нижнего основания , которую АА1 пересекает в точке А. Пересекаются.
2. Прямая BC и плоскость (AA1B1): плоскость (АА1В1) это боковая левая грань АА1В1В , которую ВС пересекает в точке В . Пересекаются.
3. Прямая CC1 и плоскость (CDD1):плоскость (CDD1) это боковая правая грань CDD1C1 , в которой СС1 лежит. Принадлежит.
4. Прямая CB1 и плоскость (BB1C1):Аналогично п.4 Принадлежит.
5. Прямая AB1 и плоскость (BCD): плоскость (BCD) это грань нижнего основания , которую ВВ1 пересекает в точке В. Пересекают .
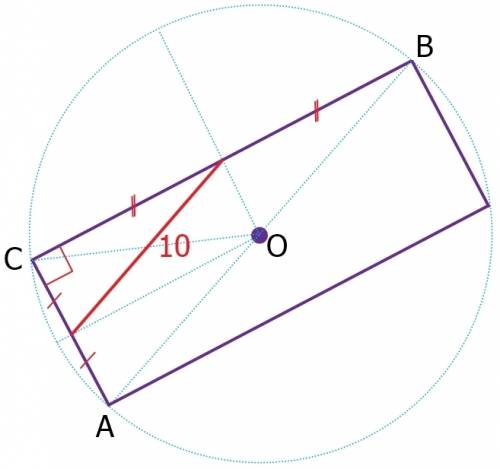
ответ: 10 (т.е. и вычислять ничего не нужно)))
а доказательство (аргументы для решения) может быть разным...
т.к. хорды по условию имеют общую точку (точку С), следовательно, ∡АСВ=90°
расстояние (которое нужно найти) называется радиусом окружности - это расстояние от центра до точки на окружности (до точки С)
известно: Прямой угол опирается на диаметр (диаметр=2*радиус).
"Расстояние между серединами" сторон треугольника - это средняя линия треугольника.
известно: Средняя линия треугольника (соединяет середины двух сторон треугольника) параллельна третьей стороне треугольника и равна ее половине. ---> диаметр=20; радиус=10...
а еще можно вспомнить: Около любого прямоугольника можно описать окружность. Радиус, перпендикулярный хорде, делит ее пополам. Диагонали прямоугольника равны.
на рисунке я провела эти радиусы и получился еще один прямоугольник (четверть большого прямоугольника), в котором диагонали равны...
38°
Объяснение:
∡7=∡3 как соответственные
∡7=38°