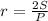 , где
, где 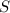 — площадь треугольника, а
— площадь треугольника, а  — его периметр.
— его периметр.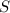 треугольника по формуле
треугольника по формуле 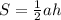 , где
, где 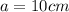 — основание, а
— основание, а  — высота, проведенная к основанию
— высота, проведенная к основанию  . Проведем к основанию
. Проведем к основанию  высоту
высоту  . Получился прямоугольный (
. Получился прямоугольный ( высота) треугольник с гипотенузой
высота) треугольник с гипотенузой  (
( — боковая стороны) и катетами
— боковая стороны) и катетами  и
и 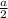 (так как треугольник равнобедренный, то высота, проведенная к основанию, является также медианой, то есть делит основание пополам, поэтому второй катет
(так как треугольник равнобедренный, то высота, проведенная к основанию, является также медианой, то есть делит основание пополам, поэтому второй катет 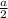 ). По теореме Пифагора найдем
). По теореме Пифагора найдем  :
:
 , найдем численное значение
, найдем численное значение  :
:

 :
: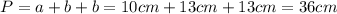

 см.
см.
перед решением нужно ещё и довольно громоздкое доказательство
площадь боковой поверхности равна произведению высоты боковой грани на полупериметр основания. Но нужно доказать, что высоты у всех граней равны.
Кроме того нужно доказать, что высота пирамиды проходит через центр вписанной окружности.
Здесь, по сути три задачи.
Площадь основания по формуле Герона = 48 кв.см
радиус вписанной окружности = площадь/п.периметр=48/16=3см
высота бок.грани = радиус/cos45=3√2
площ.боковая=3√2 * 16=48√2
ну и для полной добавить найденную площадь основания.
Для полного понимания, если вдруг захочется разобраться, читайте Атанасяна 2001, Геометрия-10, задачи 246-248