Биссектриса внутреннего угла треугольника делит противоположную сторону в отношении прилежащих сторон, образующих этот угол. Найдем длины сторон АС и ВС как модули векторов, по координатам их конца и начала.
|AC| = √((Xc-Xa)²+(Yc-Ya)²) или |AC| =√(3²+0) =3 ед.
|BC| = √((Xc-Xb)²+(Yc-Yb)²) или |BC| =√((-6)²+(-8)²) =10 ед.
Отношение сторон: k = AC/BC = 3/10 =0,3.
Координаты точки, делящей отрезок АВ, заданный координатами его начала и конца, в данном отношении k, считая от точки А (при отношении k=0,3, считая от точки А) найдем по формулам:
Xd = (Xa+k*Xb)/(1+k) и Yd = (Ya+k*Yb)/(1+k).
В нашем случае: Xd = (-1+0,3*8)/1,3) ≈ 1,08. Yd = (2+1,8)/1,3≈2,92.
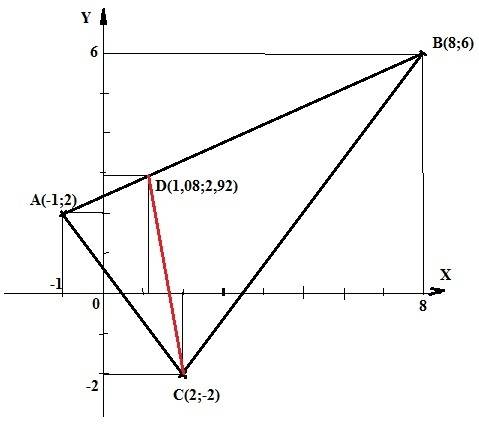
ответ: D(1,08;2;92).
P.S. Рисунок для наглядности.
Так как BC == AC, то треугольник равнобёдренный.
А так как один из боковый сторон в 2 раза больше основания, то боковая сторона равна 2AB, а основание — AB.
60дм = 600см(мне со "см" считать удобнее)
Так как боковые стороны равны, составим такое уравнение:
P = 2AB+2AB+AB
2AB + 2AB + AB = 600
Тоесть:
2x+2x+x = 600
4x + x = 600
5x = 600
x = 600/5 => x = 120
Тоесть основание(AB) равно 120см
Так как боковые равные друг другу стороны в 2 раза больше основания, то 2x = 120*2 => 2x = 240см
Сделаем сантиметры дециметрами, и всё.
AB = 12дм, BC == AC = 24дм.
P = 12+24+24
P = 60дм.
2x+2x+x = 600
4x+x = 600
5x = 600
x = 600/5 => x = 120
CA == BC = 120*2 = 240
BA = 120
P = 240+240+120 = 600
BA = 12дм(120см / 10)
BC == CA = 24дм(240см / 10)
32 дм, 24 дм
Объяснение:
Пусть а=4х дм, b=3х дм, тогда
4х*3х=768
12х²=768
х²=64; х=8
а=4*8=32 дм, b=3*8=24 дм