ответ: угол А=36°
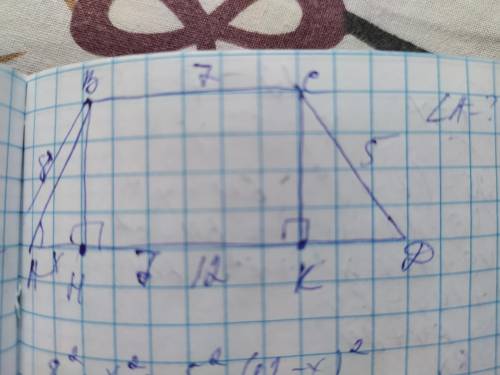
Объяснение: проведём из вершин верхнего основания к нижнему основанию АД две высоты ВН и СК. Они делят АД так что НК=ВС=7. АН+ДК=12-7=5
Высоты также образуют 2 прямоугольных треугольника АВН и СДК, в которых высоты и отрезки АН и ДК являются катетами а боковые стороны трапеции являются гипотенузой. Обе высоты имеют одну величину в обоих треугольниках. Пусть ВН=х, тогда ДК=5-х. Составим уравнение используя теорему Пифагора:
5²-(5-х)²=8²-х²
25-(25-10х+х²)=64-х²
25-25+10х-х²=64-х²
10х-х²+х²=64
10х=64
х=64/10
х=6,4
Итак: АН=6,4
Найдём угол А через косинус угла. Косинус это отношение прилежащего к углу катета к гипотенузе:
cosA=AH/AB=6,4/8=0,8≈36°
пусть авс-прямоугольный треугольник. тогда гипотенуза ас=17 см. пусть медиана выходит из точки а пусть аm — медиана(тогда bm=cm) обозначим катет bc через y, ac через x, тогда bm=cm=y\2,по теореме пифагора получаем систему и з двух уравнений первое х^2+y^2=17^2 второе x^2+(y\2)^2=15^2 отняв от первое второе получаем 3\4*(y^2)=64 y^2=256\3 y=(+\-)16\корень(3)=(+\-)16\3*корень(3) нас удовлетворяет только положительный корень(длина катета не может быть отрицательным числом), так что y=16\3*корень(3) подставив найденное значение y в первое уравнение находим х х^2+y^2=17^2 х^2+256\3=17^2 х^2=611\3 х=(+\-)корень(611\3) (нас удовлетворяет только положительное значение по той же причине что и выше) х=корень(611\3)ответ корень(611\3) и 16\3*корень(3) катеты треугольника