Дано:
<AOB и <COD
<COD внутри <AOB
AO ┴ OD; CO ┴ OB;
<AOB - <COD = 90°
Найти: <AOB и <COD.
Решение
Т.к . AO ┴ OD; CO ┴ OB,
то <AOD = 90; <COB = 90°.
<COD = <AOD - <AOC
<COD = <COB - <DOB
<COD = 90° - <AOC
<COD = 90° - <DOB
Получим
<AOC = 90° - <COD
<DOB = 90° - <COD
Следовательно <AOC = <DOB
2) По условию: <AOB - <COD = 90°
Но если от всего угла <AOB отнять <COD, то останутся два равных угла <AOC и <DOB, значит, это их сумма равна 90°.
<AOC + <DOB = 90° =>
<AOC = <DOB = 90°/2 = 45°
3) <COD = 90° - <DOB
<COD = 90° - 45°=45°
4) <AOB = <AOC + <DOB + <DOB
<AOB = 45° + 45° + 45° = 135°
ответ: <AOB - 135°; <COD =45°.

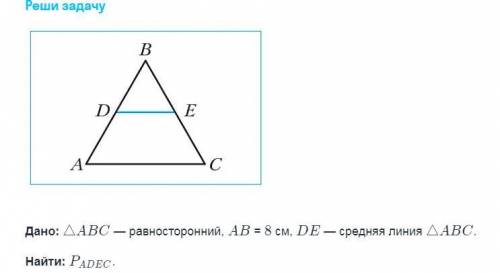
ΔABC-равносторонний,
АВ=ВС=АС=8см
DE-средняя линия
___________________
АDEС-?
AD-? EC-? DE-?
Решение.
DE-средняя линия по условию⇒ DE║АС. Геометрическая фигура, у которой 2 стороны параллельны, а 2 нет- является трапецией, значит АDEС-трапеция.
АD=DВ, ВE=EС-по условию, так как DE-средняя линия ΔАВС. Значит AD=1/2АB, AD=1/2*8=4см. EC=1/2BC, EC=1/2*8=4см.
DE=1/2AC
DE=8/2=4см.
Ответ: АDEС-трапеция, AD=4см, EC=4см, DE=4см