допустим будет треугольник ABC AB AC - катеты, BC - гипотенуза
BC=20, AC = 14
нужна найти
а) угол ACB
б) угол ABC
а) угол ACB = cosC = AC/BC = 14/20=0.7
б) угол ABC = sinB=AC/BC=cosC=0.7
если углы B и C равны, то следует что треугольник еще и равнобедренный, и значит углы равны по 45 градусов
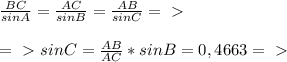
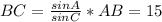
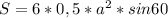, где а - сторона шестиугольника и любого из правильных треугольников. Зная площадь шестиугольника, мы находим, что 
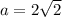. Каждая сторона шестиугольника стягивает дугу в 360\6= 60 градусов. А каждая сторона квадрата стягивает 360\4=90 градусов. Составим отношение: 60\а=90\б, где б - сторона квадрата. Выразим б. б=90а\60=
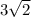. Площадь квадрата - это квадрат его стороны, поэтому его площадь будет равна 18.
первый не помню как решается
б)sin a = bc/ab bc-катет ab-гипотенуза
sin a = 17/20
sin a= 0.7
угол а=44,4 градуса
чтобы найти градусную меру синуса, на калькуляторе набираешь 0,7 нажимаешь на 2ndf и на sin получается градусная мера угла