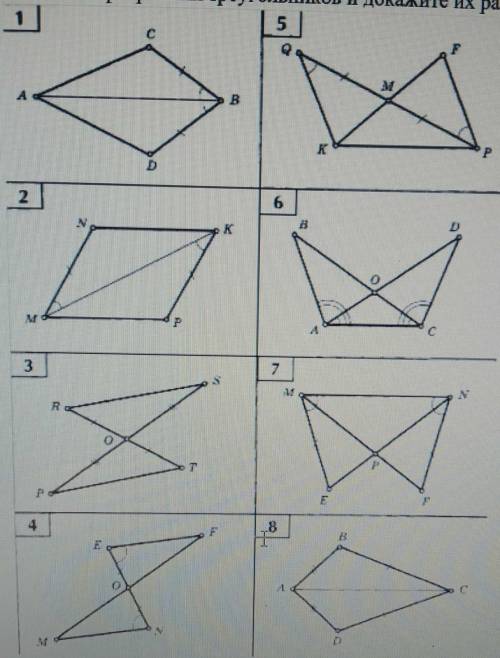
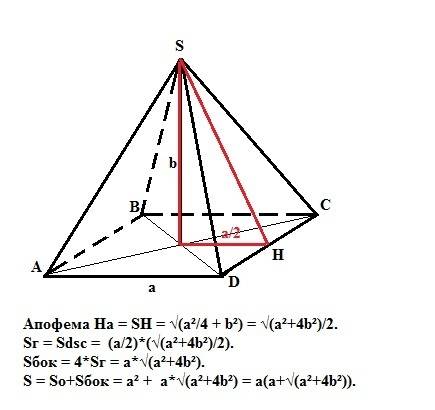
Пирамида правильная, значит в основании ее лежит квадрат, а вершина пирамиды проецируется в центр основания. Площадь полной поверхности пирамиды равна сумме площадей основания и боковой поверхности. Площадь основания нашей пирамиды равна So = a². Площадь боковой поверхности равна сумме четырех боковых граней пирамиды, каждая из которых равна Sг = (1/2)*а*На, где "а" - сторона основания, а "На" - апофема (высота) грани. Апофему грани найдем по Пифагору из прямоугольного треугольника, образованного высотой пирамиды, половиной стороны основания (катеты) и апофемой (гипотенуза). На = √(a²/4 + b²) = √(a²+4b²)/2.
Тогда площадь одной грани равна Sг = (a/2)*(√(a²+4b²)/2), площадь боковой поверхности пирамиды равна 4*Sг = а* √(a²+4b²).
Площадь полной поверхности пирамиды равна
S = a²+а* √(a²+4b²) = a(a+√(a²+4b²)).
Явная опечатка. не 1 см, а 11 см. т.к. с такими данными не существует треугольника. исправьте условие.
теперь решение.
Если соединить середины сторон данного треугольника, то получите треугольник, состоящий их средних линий данного треугольника.
Каждая средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны, поэтому стороны треугольника, вершинами которого являются середины сторон данного треугольника, будут 5/2=2.5/см/, 7/2=3.5/см/, 11/2=5.5/см/
ответ 2.5см, 3.5 см, 5.5 см.