
Равенство треугольников АОК и ВОF доказано.
Объяснение:
Требуется доказать, что треугольники AOK и DOF равны.
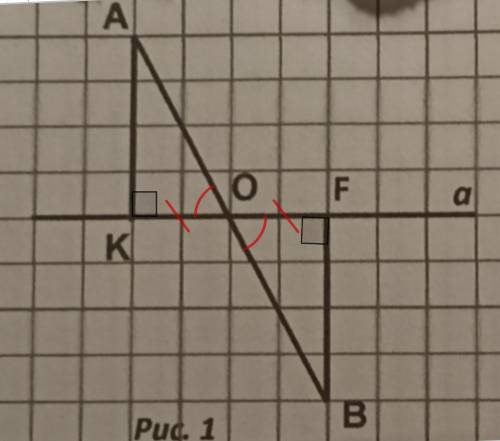
Дано: АК ⊥ а; BF ⊥ a;
AB ∩ a = O;
KO = OF.
Доказать: ΔАОК = ΔВОF.
Доказательство:
Рассмотрим ΔАОК и ΔВОF.
АК ⊥ а; BF ⊥ a (по условию)
⇒ ΔАОК и ΔВОF - прямоугольные.
KO = OF (условие);
∠АОК = ∠ВОF (вертикальные)
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники равны.⇒ ΔАОК = ΔВОF (по катету и прилежащему острому углу)
Равенство треугольников АОК и ВОF доказано.
2) Правильный треугольник - это треугольник у которого все стороны равны(равносторонний).
3)У треугольника три биссек.
4)...если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
5)и KM=EG
6) треуг. тупоугольный.
7)Треугольником называется геометрическая фигура состоящая из трех точек не лежащих на одной прямой и трех отрезков, которые соед. эти точки.
8)Квадрат
9)0
10)Если два угла и сторона между ними одного треуг соответ. равны двум углам и стороне между ними другого треуг, то такие треуг равны.
11)E=B
12)треугольник прямоугольный, а два острых угла в сумме дают 90 градусов