Дан треуг. равнобедренный, но поскольку угол при основании ВАС=60, то треуг. является равносторонним и все его углы 60 градусов.
Теперь, на продолжении стороны АС обозначим точку О, угол ВСО смежный с углом АСВ. ВСО=180-60=120. Так кам СF бисектриса, то угол BCF=120/2=60. Теперь мы имеем две прямые АВ и CF и секущую ВС. Угол АВС=BCF=60 (это мы уже нашли), а эти углы являются накрестлежащими, а по теореме о двух паралельных прямых и секущей, если накрестлежащие углы равны, то эти прямые параллельны, следовательно, АВ паралельна CF.
Доказано.
Если искать длину, то только окружности, а не круга.
ABCD-квадрат. Окружность проходит через точки А и В и касается точки К на противоположной стороне, причем будет выполняться равенство СК=DK=6см. Теперь через точку К проведем прямую, параллельную сторонам ВС и AD. Эта прямая пересечет сторону ВС в точке Е такой, что АЕ=ВЕ=6см. И эта прямая также пересечет окружность в точке М. МК-является диаметром нашей окружности, а формула длины окр-ти l=Пd.
Найдем ВК^2=BC^2+CK^2=144+36=180
Треугольник (МВК), одна сторона которого является диаметром окр-ти, а противолежащая вершина лежит на этой окр-ти, является прямоугольным, а эта вершина и будет вершиной прямого угла.
Пусть МЕ=х, тогда из треуг. МВК:
ВМ^2=(12+x)^2-180, а из треуг. МЕВ ВМ^2=36+x, приравняем, получим
(12+x)^2-180=36+x
144+x^2+24x-180=36-x^2
24x=72
x=3 см, МЕ=3см, d=КМ=12+3=15см
l=3,14*15=47,1см
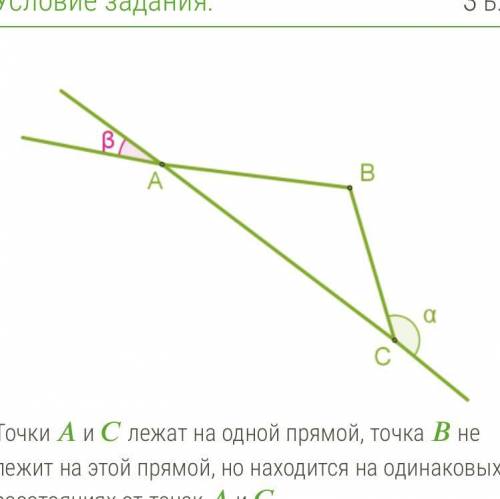
Так как расстояния ВА и ВС одинаковы, следовательно, треугольник равнобедренный. Углы α - внешний угол треугольника и в сумме с внутренним углом C, смежным с ним, составляет 180°. Следовательно, <C = 180°-152°=28°.
Углы при основании равнобедренного треугольника равны. Следовательно, <A=<C=28° a <B=180° - 2*28° = 124°. Треугольник АВС тупоугольный.
Углы β и <А вертикальные, следовательно, они равны.
ответ: 1. Треугольник АВС тупоугольный, равнобедренный. 2 ∡β = 28°.