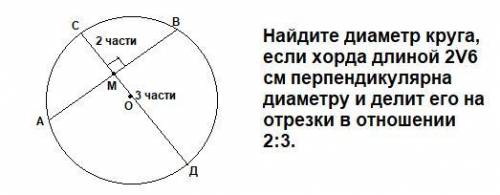
Найдите диаметр круга, если хорда длиной 2V6 см перпендикулярна диаметру и делит его на отрезки в отношении 2:3.
Объяснение:
ΔОМА=ΔОМВ как прямоугольные по двум катетам ОМ-общий, ОА=ОВ как катеты ⇒МА=МВ=2√6:2=√6 (см)
По т. об отрезках пересекающихся хорд АМ*МВ=СМ*МД
Т.к. СМ/МД=2/3 , то МД=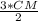 
. Получим √6*√6= СМ* .
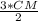СМ²=4, СМ=2 см .
Тогда МД=3 см , поэтому диаметр равен d= СМ+МД=2+3=5 (см).
d=5 см
=====================
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
АЕ * БЕ = СЕ * ЕД
Пусть СЕ = х, тогда:
0.2 * 0.5 = х*(0.65 -х)
0.1= 0.65х - х^2
х^2 - 0.65х + 0.1= 0
20х^2 - 13х + 2 =0
х1= 0.4
х2 = 0.25
ЕД = 0.4
ЕС = 0.25
Или наоборот