В самом деле, мы УЖЕ доказали, что О1М/О2М = ВМ/СМ. Для прямоугольного треугольника этого вполне достаточно.
Для радиуса вписанной окружности r треугольника АВС тоже можно записать соотношение подобия (пропорциональности) с треугольником ВСМ.
r/r1 = c/b (b - гипотенуза в треугольнике ВСМ).
Но c/b = d/(r1*корень(2)) (отношение гипотенузы к малому катету в треугольниках АВС и О1О2М).
поэтому
r/r1 = d/(r1*корень(2));
r = d/корень(2);
ну, d = 1 по условию.
Всё так удачно складывается именно потому, что h и b играют как-бы двойную роль - h - малый катет в СМА и большой в ВМС, а b - малый катет в АВС, и гипотенуза в ВМС.
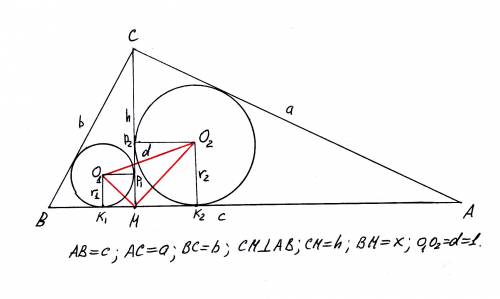
Ход решения задачи.
1.
Провести через вершину меншего основания прямую, паралельную боковой стороне трапеции.
Получим на основании 2 отрезка, один из которых равен 2, другой - 1см( равный меньшему основанию)
2.
Обозначить отрезок между основанием высоты и большим углом у основания х
Составить 2 выражения для нахождения высоты трапеции (из того же угла), для чего опустить эту высоту на большее основание и приравнять их.
Получим
h²=()²-х²
h²=4² - (2-х)²
(2√3)²-х²=4² - (2-х)²
Решив это уравнение. найдем, что х=0.
Отсюда эта трапеция - прямоугольная, и углы при меньшей боковой стороне - прямые.
h=2√3
Косинус нужного угла =2:4=0,5
Найдите угол по таблице косинусов.
Этот угол равен 60º.
(2+6);(-9+3)=(8;-6)
Длина вектора
√a²+b²=8²+(-6)²=√100=10см
ответ 10см