а) Пусть катет равен х см, тогда по теореме Пифагора :
х² + х² = 8²
2х² = 64
х² = 32
х = √32 = 4√2
Площадь прямоугольного треугольника можно найти по формуле S = 0.5 * a * b (а и b это катеты)
S = 0.5 * 4√2 *4√2 = 4*4 = 16 (см²)
б) 1,4дм = 14 см
Пусть катет будет равен х см, тогда по теореме Пифагора :
х² + х² = 14²
2х² = 196
х² = 98
х = √98 =7√2 см
S = 0.5*7√2 *7√2 = 7*7 = 49см² = 0.49 дм²
в)пусть катет также будет равен х м , по теореме Пифагора :
х² + х² = с²
2х² = с²
х² = с²/2
х = с/√2
S = 0.5 * (c/√2) * (c/√2) = c²/4 (м²)
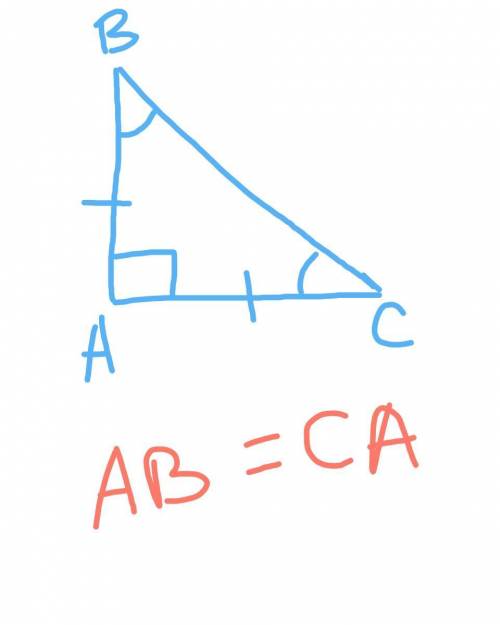
шестигранник разделим не 6 треугольников, причем 1.5 см - это будет диаметр вписанной окружности.Тогда радиус вписанной окружности = 0,75 см.
Рассмотрим один такой треугольник.
Угол при центре окружности равен 360/6=60 град, значит треугольник равнобедренный, тогда углы при основании = (180-60)/2=60град - значит треугольник равносторонний, тогда радиус описанной окружности - высота этого треугольника и биссектриса для угла при центре окружности, тогда углы в таком треугольнике будут 30, 60, 90, значит
Пусть гипотенуза - 2х, тогда один катет, напротив угла60=0,75, а второй катет напротив угла 30=половина гипотенузы=х , тогда
по т Пиф 
Тогда площадь шестиугольника=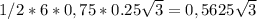
см квадратных
вот и всё
Продлим биссектрисы до пересечения с прямой основания LM.
△AEL~△NEK (по накрест лежащим при LM||KN)
AL/KN =EL/EK =1/7 => AL=3
Аналогично BM/KN=2/7 => BM=6
A=N/2 (накрест лежащие) => △AMN - равнобедренный, MN=AM=9
Аналогично KL=LB=12
Опустим высоты (h) на большее основание KN.
CD=LM=6
Пусть KC=x, тогда DN=15-x
Теорема Пифагора для △KLC и △NMD
144 =h^2 +x^2
81 =h^2 +(15-x)^2
Решаем
63=x^2 -(15-x)^2 => x =(225+63)/30 =9,6
h =√(144-92,16) =7,2
S(KLMN) =1/2 (KN+LM)*h =1/2 *27 *7,2 =97,2