ответ:1. Если KM = NJ, ML = JR, __М= J__, то ΔKML=ΔNJR по первому признаку- по двум сторонам и углу между ними
2. KM = NJ, ML = JR,_KL=NR_, то ΔKML=ΔNJR по третьему признаку-по трем сторонам.
3. KL = NR, ∡ K = ∡ N, _∡ L= ∡ R, то
ΔKML=ΔNJR по второму признаку-по стороне и двум прилежащим углам.
4. KL = NR, ∡ K = ∡ N,_KM=NJ__ , то ΔKML=ΔNJR по первому признаку- по двум сторонам и углу между ними
5. ∡ M = ∡ J, ∡ L = ∡ R, _ML =NR_ , то ΔKML=ΔNJR по второму признаку-по стороне и двум прилежащим углам.
Формула вычисления стороны квадрата, зная описанный радиус: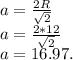
Формула вычисления радиуса вписанной окружности в квадрат, зная его сторону:
Вывод: Сторона квадрата равна: 16.97; радиус вписанной окружности — 8.5.
8.Формула вычисления радиуса описанной окружности, зная сторону правильного треугольника:
Длина круга равна:
Не поняла, площадь какого круга надо найти, так что найду площади и вписанной, и описанной окружности.
Формула вычисления площади описанной окружности такова:
Формула вычисления площади вписанной окружности такова: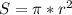
Радиус вписанной окружности в правильный треугольник, мы найдём по стороне этого же треугольника:
Площадь окружности равна:
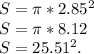
9.Формула вычисления стороны правильного треугольника, зная радиус описанной окружности:
Радиус вписанной окружности равен:
Площадь окружности равна: