Сумма 4-х углов четырехугольника равна 360. Поскольку в паралелограмме противоположные углы равны, значит сумма двух соседних углов равна 180. Отнимаем 46 и делим на 2, получаем один угол 67, второй (+46) равен 113.
можно так:
Такие углы не могут быть противолежащими, так как они не равны. Значит, они прилежащие и их сумма равна 180°. Пусть один из углов равен х, тогда другой равен х+46°, по условию. Следовательно х+(х+46)=180
2х+46=180
2х=180-46
2х=134
х=67-первый,а второй х+46°=67+46=113 градусов
Номер 2
а)1.Если верить цифрам,то ошибка на чертеже,что АС=СВ и треугольник является равнобедренным,т к если угол при вершине равен 50 градусов,один угол при основании 70 градусов,а третий должен быть 60 градусов,а это значит,что треугольник не равнобедренный
а)2.Если взять под сомнение величины углов,то внешний должен быть 140 градусов,а не 130.Или углы при основании должны быть равны по 65 градусов,а не по 70.
Номер 2
б)На чертеже обозначено,что треугольник равносторонний,а это значит,что не только стороны равны между собой,но и каждый угол равен 60 градусов,судя по чертежу-внутренний угол D равен
<D=180-130=50 градусов
Номер 2
в)Ксли треугольник ОМN равнобедренный,как указано на чертеже,то углы при основании должны быть равны
(180-160):2=10 градусов
Внутренний угол N равен
<N=180-165=15 градусов-нестыковочка!!
Номер 2
г)Сумма внутренних углов треугольника равна 180 градусов,в этом же треугольнике сумма
90+30+40=160 градусов,такого не может быть
Номер 3
<А=Х
<В=4Х
<С=4Х-90
Х+4Х+4Х-90=180
9Х=180+90
9Х=270
Х=270:9
Х=30
<А=30 градусов
<В=30•4=120 градусов
<С=120-90=30 градусов
Проверка
30+120+30=180 градусов
Угол А и угол С-углы при основании равнобедренного треугольника
<А=<С=30 градусов,отсюда вытекает,что
АВ=ВС,как боковые стороны равнобедренного треугольника
Объяснение:
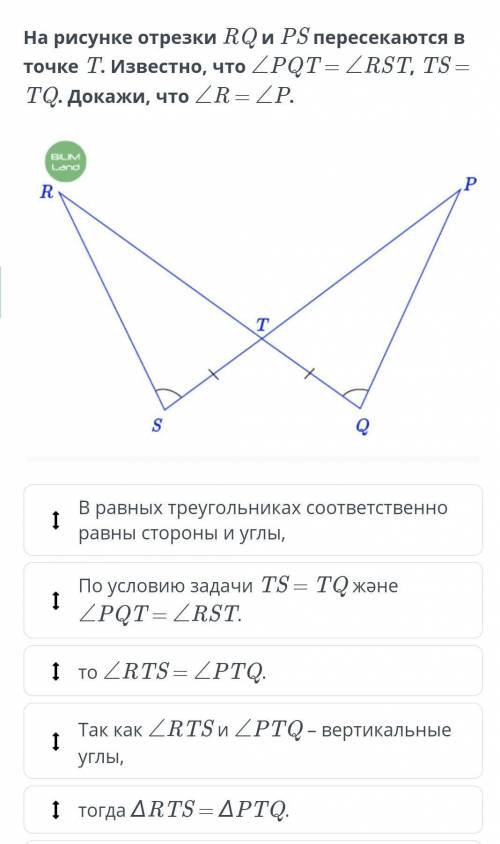
По условию задачи TS = TQ және ∠PQT = ∠RST.
Так как ∠RTS и ∠PTQ – вертикальные углы,
то ∠RTS = ∠PTQ.
Одна сторона треугольника и прилежащие к ней два угла соответственно равны,
тогда ∆RTS = ∆PTQ.
В равных треугольниках соответственно равны стороны и углы,
следовательно, ∠R = ∠P.
Объяснение:
это правильно