1.Треугольник ABD = 1. Угол ВАD = CAD
2. BDA=CDA
треугольнику ADC
3.AD - общая сторона.
Второй признак равенства
треугольников
2.
Углы 1 и 2 вертикальные, значит они
равны, следовательно треугольники, по двум углам и стороне, равны. Исходя из этого, СD делиться попалам в точки О
3.
<АСО=<1 как вертикальные углы.
<BDO=<2 как вертикальные углы. Но
<1=<2, значит
<ACO=<BDO.
<AOC=<BOD как вертикальные углы.
Значит, треугольники АСО и BDO
равны по второму признаку: сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней
углам другого треугольника: - ОС=ОD по условию;
- <ACO=<BDO как доказано выше;
.<AOC=<BOD как доказано выше. У равных треугольников АСО и BDO равны соответственные углы А и В.
4.
3.
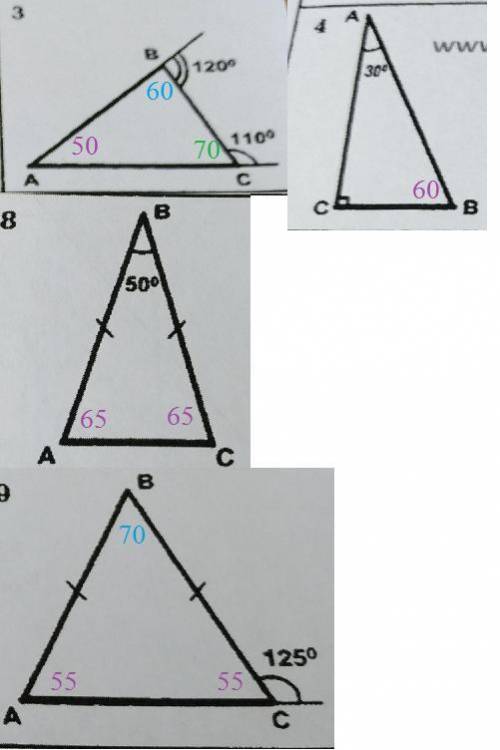
Cумма смежных углов 180 градусов.
Если один угол 120°, то второй 180°-120°=60°
Если один угол 110°, то второй 180°-110°=70°
Сумма углов треугольника АВС равна 180 градусов, два угла 60° и 70°, значит угол А равен 180°-60°-70°=50°
4.
Сумма острых углов прямоугольного треугольника равна 90°
Если один угол 30°, то второй 90°-30°=60°
8. Треугольник равнобедренный (АВ=ВС), значит углы при основании равны
Сумма углов треугольника равна 180°
180°-50°=130° - приходится на два угла при основании
130°:2=65°
9.
Cумма смежных углов 180 градусов.
Если один угол 125°, то второй 180°-125°=55°
Треугольник равнобедренный (АВ=ВС), значит углы при основании равны.
∠А=∠С=55°
Сумма углов треугольника равна 180°
180°-55°-55°=70° - третий угол треугольника
5:2=2,5 2,5✓, 25,2,5✓