Обозначим :
Н - высота пирамиды
h - высота основания пирамиды
r -радиус окружности, вписанной в основание
а - сторона основания
Решение
а) высота пирамиды Н = L· sinβ
б) проекция апофемы на плоскость основания -это радиус вписанной окружности r = L · cosβ.
в) сторона основания пирамиды а = 2r/tg 30° = 2L· cosβ/(1/√3) =
= 2√3 · L·cosβ
г) площадь основания пирамиды Sосн = 0.5h·a, где h = a·cos30°.
Тогда Sосн = 0.25a²·√3 = 0.25 · √3 · (2√3 · L·cosβ)² = 3√3L² · cos²β
д) Площадь боковой поверхности пирамиды
Sбок = 3 · 0,5 · L · a = 1.5L · 2√3 · L·cosβ = 3√3 · L² · cosβ
e) площадь полной поверхности пирамиды:
Sполн = Sосн + Sбок = 3√3 · L² · cos²β + 3√3 · L² · cosβ =
= 3√3 · L² · cosβ · (cosβ + 1)
Подробнее - на -
3) Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180°.
Так как углы, взятые в порядке следования относятся как 1:3:4 , то ∠А=х , ∠В=3х , ∠С=4х и ∠А+∠С=х+4х=5х=180° , х=36° .
∠А=36° , ∠В=3*36°=108° , ∠С=4*36°=144°
Сумма внутренних углов четырёхугольника равна 360°.
∠D=360°-36°-108°-144°=72°
Или ∠В+∠D=5х , ∠D=5x-∠B=3x-3x=2x , 2x=2*36°=72° .
4) Сторона правильного треугольника равна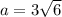 .
.
Радиус вписанной окружности в прав. тр-к равна 1/3 его высоты, то есть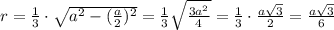 .
.
Сторона прав.четырёхугольника - квадрата, описанного около окружности, равна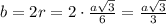 .
.
Периметр квадрата равен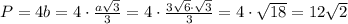 см.
см.