1. Понятие многоугольника Периметр. 2. Компоненты многоугольника (соседние вершины, смежные стороны, диагональ) 3. Внутренняя и внешняя область многоугольника. 4. Понятие выпуклого многоугольника. 5. Формула суммы углов выпуклого многоугольника. 6. Формула суммы внешних углов многоугольника. 7. Противоположные углы и стороны. 8. Сумма углов выпуклого четырехугольника. 9. Определение параллелограмма. 10. Свойства параллелограмма (2). 11. Признаки параллелограмма (3) 12. Свойство биссектрисы угла параллелограмма. 13. Свойство параллелограмма. 14. Определение трапеции. 15, Компоненты трапеции. 16. Свойство средней линии трапеции. 17. Определение равнобедренной трапеции. 18. Свойства равнобедренной трапеции (2). 19. Определение прямоугольной трапеции. 20. Теорема Фалеса 21. Определение прямоугольника. 22. Свойство прямоугольника (обратное свойство). 23. Определение ромба 24. Свойство ромба. 25. Определение квадрата (2). 26. Свойства квадрата. 27. Понятия об осевой и центральной симметрии. 28. Задачи на построение пересечения биссектрис углов смежных
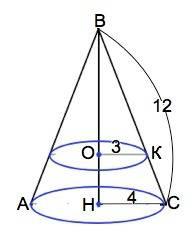
Плоскость, пересекающая боковую поверхность конуса по кругу, отсекает от первоначального конуса меньший конус с вершиной А. Меньший конус образован от вращения меньшего прямоугольного треугольника AO₁B₁, где AO₁ - катет и высота меньшего конуса (искомое расстояние от вершины до плоскости пересечения), О₁В₁ - второй катет - равен радиусу (r) окружности пересечения бОльшего конуса плоскостью. Длина этой окружности L=6π. АB₁ - образующая меньшего конуса.
Угол ОАВ совпадает с углом О₁АВ₁. Угол АОВ и угол АО₁В₁ - прямые ⇒ Угол ABO = Углу АВ₁О₁ ⇒ равны тангенсы углов ABO и АВ₁О₁
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему.
AO 12
Tg угла ABO= = = 3
OB 4
AO₁
Tg угла АB₁O₁ = = 3
O₁B₁
AO₁ = 3 * O₁B₁
Длина окружности = 2 * π * r = 6π ⇒ r = 3 (cм) ⇒ O₁B₁ = 3 (см)
AO₁ = 3 * 3 = 9 (см)
Расстояние от вершины конуса до сечения равно 9 см