10 см
Объяснение:
Радиус вписанной окружности равен половине высоты этой трапеции (высота равна диаметру.)
В трапецию можно вписать окружность, если суммы ее противоположных сторон равны.
10+40=50 - сумма боковых сторон
50:2=25 - боковая сторона.
Опустим из тупого угла высоту на большее основание.
Получим прямоугольный треугольник с гипотенузой 13, катетом, равным полуразности оснований и равным
(40-10) : 2 = 15, и вторым катетом - высотой трапеции.
По теореме Пифагора диаметр окружности равен
√ (25²-15²) = 20 см
Радиус равен половине диаметра
20:2=10 см
ответ: радиус вписанной окружности в трапецию равен 10 см
т о биссектрисе
BE/EA =BC/CA =4/5
т Менелая
AD/DC *CF/FE *EB/BA =1 => 1/1 *CF/FE *4/9 =1 => CF/FE =9/4
Площади треугольников с равными высотами относятся как основания.
S(AEF)=x, S(CDF)=S(ADF) =y
S(AFC)/S(AEF) =CF/FE =9/4 =2y/x => S(AEF)/S(CDF) =x/y =8/9
Другое решение
BF/FD =BC/CD =4 :5/2 =8/5 (т о биссектрисе)
S(BCF)/S(CDF) =BF/FD =8/5 => S(CDF)=5/8 S(BCF)
S(ABD)=S(CBD), S(AFD)=S(CFD) => S(BCF)=S(BAF)
BE/EA =BC/CA =4/5 (т о биссектрисе)
S(BFE)/S(AEF) =BE/EA =4/5 => S(AEF) =5/9 S(BAF)
S(AEF)/S(CDF) =5/9 :5/8 =8/9
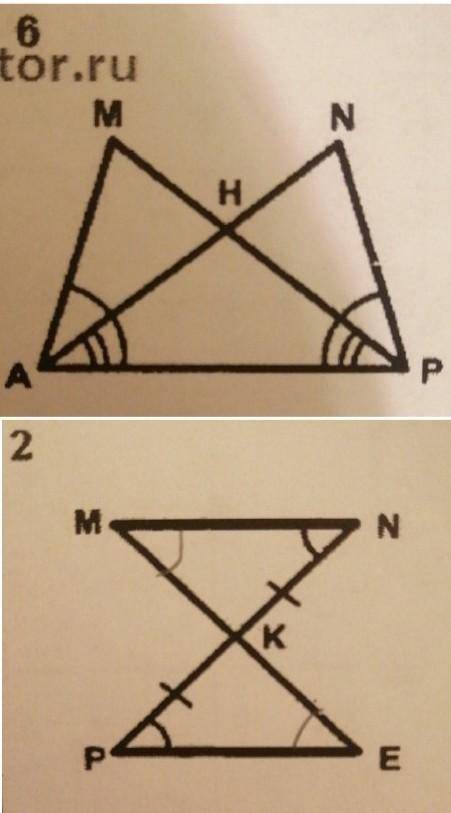
триугольник РКЕ и МНК равен с триугольником АНР